搜索
【题目】已知：如图，在⊙O中，直径AB的长为10cm,弦AC的长为6cm,∠ACB的平分线交⊙O于点D,求BC,AD和BD的长。
参考答案：
【答案】
cm, AD=BD=
cm
【解析】试题分析：
如图，连接BD，由AB是⊙O直径可得∠ACB=∠ADB=90°，结合AC=6，AB=10由勾股定理即可解得：BC=8；由CD平分∠ACB可得∠ACD=∠BCD，从而可得
，进一步可得AD=BD，这样△ABD是等腰直角三角形，结合AB=10，由AD=sin∠45°×10即可求出AD和BD的长.
试题解析：
∵AB为⊙O直径，
∴∠ACB=∠ADB=90°
在Rt△ACB中，
(cm)
∵CD平分∠ACB，
∴∠ACD=∠BCD，
∴
，
∴AD=BD
在等腰Rt△ADB中，
AD=BD= 
(cm)
∴BC=8cm，AD=BD=
cm.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,是二次函数y=ax2+bx+c的部分图象.
(1)结合图象信息,求此二次函数的表达式;
(2)当y＞0时，直接写出x的取值范围： 。
-
科目： 来源： 题型：
查看答案和解析>>【题目】股民铭铭上星期五买进萱萱公司的股票1000股，每股27元，下表为本周内每日该股票的涨跌情况(单位：元)(注：用正数记股价比前一日上升数，用负数记股价比前一日下降数)
(1)星期二收盘时，每股是多少元?
(2)本周内最高价是每股多少元?最低价每股多少元?
(3)已知铭铭买进股票时付了购买金额0.1%的手续费，卖出时需付成交额0.15%的手续费和0.1%的交易税，如果铭铭在星期五收盘前将全部股票卖出，他的收益(获利)情况如何?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴上有三个点A、B、C，表示的数分别是－4、－2、3，请回答：
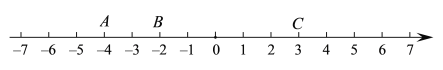
(1)若C、B两点的距离与A、B两点距离相等，则需将点C向左移动________个单位；
(2)若移动A、B、C三点中的两点，使三个点表示的数相同，移动方法有________种，其中移动所走的距离之和最小的是________个单位；
(3)若在B处有一小青蛙，一步跳一个单位长，小青蛙第一次先向左跳一步，第2次向右跳3步，第3次向再向左跳5步，第4次再向右跳7步……，按此规律继续下去，那么跳第100次时落脚点表示的数是________；
(4)若有两只小青蛙M、N，它们在数轴上的点表示的数分别为整数x、y，且|x－2|+|y+3|=2，求两只青蛙M、N之间的距离.
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程：(1)
； （2）
.【答案】（1）x1 =1 ，x2=
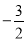； (2) x1 =-1，x2=
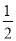.【解析】试题分析：
根据两方程的特点，使用“因式分解法”解两方程即可.
试题解析：
（1）原方程可化为：
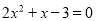，方程左边分解因式得：
，
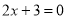或
，解得：
， 
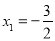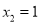.（2）原方程可化为：
，即
，∴
，∴
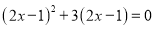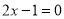或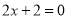
，解得：
.【题型】解答题
【结束】
20【题目】已知x1，x2是关于x的一元二次方程x2－2(m＋1)x＋m2＋5＝0的两实根．
(1)若(x1－1)(x2－1)＝28，求m的值；
(2)已知等腰△ABC的一边长为7，若x1，x2恰好是△ABC另外两边的边长，求这个三角形的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】商场某种商品进价为 70 元，当售价定为每件 100 元时，平均每天可销售 20 件.经调查发现，每件商品每降价 1 元，商场平均每天可多售出 2 件.若商场规定每件商品的利润率不低于 30%，设每件商品降价 x 元.
(1)商场日销售量增加 件，每件商品盈利 元(用含 x 的代数式表示);
(2)在上述条件不变、销售正常情况下，每件商品降价多少元时，日盈利可达到 750 元?
-
科目： 来源： 题型：
查看答案和解析>>【题目】有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的纪录如下：
回答下列问题：
（1）这8筐白菜中最接近标准重量的这筐白菜重__________千克；
（2）与标准重量比较，8筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.6元，则出售这8筐白菜可卖多少元？
相关试题
