【题目】(本题满分8分)
在四边形ABCD中,对角线AC、BD交于点O.若四边形ABCD是正方形如图1:则有AC=BD,AC⊥BD.
旋转图1中的Rt△COD到图2所示的位置,AC’与BD’有什么关系?(直接写出)
若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC’与BD’又有什么关系?写出结论并证明.

参考答案:
【答案】图2结论:AC′=BD′,AC′⊥BD′,理由见解析;图3结论:BD′=![]() AC′,AC′⊥BD’,理由见解析.
AC′,AC′⊥BD’,理由见解析.
【解析】
试题分析:图2:根据四边形ABCD是正方形,得到AO=OC,BO=OD,AC⊥BD,根据旋转的性质得到OD′=OD,OC′=OC,∠D′OD=∠C′OC,等量代换得到AO=BO,OC′=OD′,∠AOC′=∠BOD′,根据全等三角形的性质得到AC′=BD′,∠OAC′=∠OBD′,于是得到结论;
图3:根据四边形ABCD是菱形,得到AC⊥BD,AO=CO,BO=DO,求得OB=![]() OA,OD=
OA,OD=![]() OC,根据旋转的性质得到OD′=OD,OC′=OC,∠D′OD=∠C′OC,求得OD′=
OC,根据旋转的性质得到OD′=OD,OC′=OC,∠D′OD=∠C′OC,求得OD′=![]() OC′,∠AOC′=∠BOD′,根据相似三角形的性质得到BD′=
OC′,∠AOC′=∠BOD′,根据相似三角形的性质得到BD′=![]() AC′,于是得到结论.
AC′,于是得到结论.
试题解析:图2结论:AC′=BD′,AC′⊥BD′,
理由:∵四边形ABCD是正方形,
∴AO=OC,BO=OD,AC⊥BD,
∵将Rt△COD旋转得到Rt△C′OD′,
∴OD′=OD,OC′=OC,∠D′OD=∠C′OC,
∴AO=BO,OC′=OD′,∠AOC′=∠BOD′,
在△AOC′与△BOD′中,
 ,
,
∴△AOC′≌△BOD′,
∴AC′=BD′,∠OAC′=∠OBD′,
∵∠AO′D′=∠BO′O,∠O′BO+∠BO′O=90°,
∴∠O′AC′+∠AO′D′=90°,
∴AC′⊥BD′;

图3结论:BD′=![]() AC′,AC′⊥BD’
AC′,AC′⊥BD’
理由:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∵∠ABC=60°,
∴∠ABO=30°,
∴OB=![]() OA,OD=
OA,OD=![]() OC,
OC,
∵将Rt△COD旋转得到Rt△C′OD′,
∴OD′=OD,OC′=OC,∠D′OD=∠C′OC,
∴OD′=![]() OC′,∠AOC′=∠BOD′,
OC′,∠AOC′=∠BOD′,
∴![]() ,
,
∴△AOC′∽△BOD′,
∴![]() ,∠OAC′=∠OBD′,
,∠OAC′=∠OBD′,
∴BD′=![]() AC′,
AC′,
∵∠AO′D′=∠BO′O,∠O′BO+∠BO′O=90°,
∴∠O′AC′+∠AO′D′=90°,
∴AC′⊥BD′.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直线y=
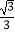 x+1上取一点A1 , 以O、A1为顶点作等一个等边三角形OA1B1 , 再在直线上取一点A2 , 以A2、B1为顶点作第二个等边三角形A2B1B2 , …,一直这样做下去,则B1点的坐标为 , 第10个等边三角形的边长为 .
x+1上取一点A1 , 以O、A1为顶点作等一个等边三角形OA1B1 , 再在直线上取一点A2 , 以A2、B1为顶点作第二个等边三角形A2B1B2 , …,一直这样做下去,则B1点的坐标为 , 第10个等边三角形的边长为 . 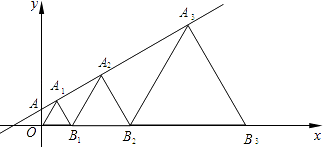
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形三边满足(a+b)2﹣c2=2ab,则这个三角形是______三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一根竹竿,不知道它有多长.把竹竿横放在一扇门前,竹竿长比门宽多4尺;把竹竿竖放在这扇门前,竹竿长比门的高度多2尺;把竹竿斜放,竹竿长正好和门的对角线等长.问竹竿长几尺?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列角度中,不能成为多边形内角和的是( )
A. 600° B. 720° C. 900° D. 1800°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2+x3=x5
B.(x3)3=x6
C.xx2=x2
D.x(2x)2=4x3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y关于x的一次函数y=(2m2﹣32)x3﹣(n﹣3)x2+(m﹣n)x+m+n.
(1)若该一次函数的y值随x的值的增大而增大,求该一次函数的表达式,并在如图所示的平面直角坐标系中画出该一次函数的图象;
(2)若该一次函数的图象经过点(﹣2,13),求该函数的图象与坐标轴围成的三角形的面积.
相关试题

