【题目】已知y关于x的一次函数y=(2m2﹣32)x3﹣(n﹣3)x2+(m﹣n)x+m+n.
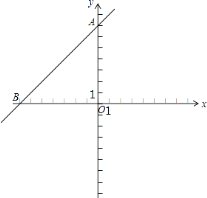
(1)若该一次函数的y值随x的值的增大而增大,求该一次函数的表达式,并在如图所示的平面直角坐标系中画出该一次函数的图象;
(2)若该一次函数的图象经过点(﹣2,13),求该函数的图象与坐标轴围成的三角形的面积.
参考答案:
【答案】
(1)解:∵y关于x的一次函数y=(2m2﹣32)x3﹣(n﹣3)x2+(m﹣n)x+m+n,
∴2m2﹣32=0,n﹣3=0,
解得:m=±4,n=3,
又∵该一次函数的y值随x的值的增大而增大,
∴m﹣n>0,
则m=4,n=3,
∴该一次函数的表达式为:y=x+7,
如图所示:
(2)解:∵该一次函数的图象经过点(﹣2,13),
∴y=﹣7x﹣1,
如图所示:
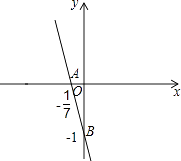 ,
,
当x=0,则y=﹣1,当y=0,则x=﹣ ![]() ,
,
故该函数的图象与坐标轴围成的三角形的面积为: ![]() ×1×
×1× ![]() =
= ![]()
【解析】(1)直接利用一次函数增减性结合一次函数的定义得出m,n的值进而画出图象;(2)利用一次函数图象上点的坐标特征得出一次函数解析式,进而求出图象与坐标轴围成的三角形的面积.
【考点精析】通过灵活运用一次函数的性质和确定一次函数的表达式,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
在四边形ABCD中,对角线AC、BD交于点O.若四边形ABCD是正方形如图1:则有AC=BD,AC⊥BD.
旋转图1中的Rt△COD到图2所示的位置,AC’与BD’有什么关系?(直接写出)
若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC’与BD’又有什么关系?写出结论并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列角度中,不能成为多边形内角和的是( )
A. 600° B. 720° C. 900° D. 1800°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2+x3=x5
B.(x3)3=x6
C.xx2=x2
D.x(2x)2=4x3 -
科目: 来源: 题型:
查看答案和解析>>【题目】乘火车从A站出发,沿途经过1个车站方可到达B站,那么在A、B两站之间能安排不同的车票种.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正n边形的一个内角为135°,那么n的值为( )
A.12B.10C.8D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
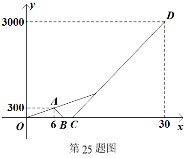
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
⑴小亮在家停留了 分钟.
⑵求小亮骑单车从家出发去图书馆时距家的路程y(米)与出发时间x(分钟)之间的函数关系式.
⑶若小亮和姐姐到图书馆的实际时间为m分钟,原计划步行到达图书馆的时间为n分钟,则n-m= 分钟.
相关试题

