【题目】蚂蚁从点O出发,在一条直线上来回爬行.假定向右爬行的路程记为正数,向左爬行的路程记为负数,则爬过的各段路程依次记为(单位:cm):+5,-3,+10,-8,-6,+12,-10.
![]()
(1)蚂蚁最后是否回到出发点O?
(2)蚂蚁离开出发点O最远是多少?
(3)在爬行过程中,如果每爬行1奖励一粒糖,那么蚂蚁一共得到多少粒糖?
参考答案:
【答案】(1)回到了出发点;(2)12cm;(3)54粒
【解析】试题分析:(1)要想知道蚂蚁是否能回到原点,关键是看它分别向左向右的爬行路程之和是否为0.
(2)离出发点最远的距离,就是将小虫爬行的路程依次相加,看看走到哪一段是最大值.
(3)要求一共得到多少米粒,即就是问蚂蚁一共爬行了多少路程即可.
解:(1)将所有记录的路程相加,得
(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)
=((+5)+(+10)+(+12))+((-3)+(-8)+(-6)+(-10))
=27+(-27)
=0(cm).
即左右爬行的路程相同, 蚂蚁最后回到出发点O.
(2)根据记录的数据,得
蚂蚁离出发点最远的距离是(+5)+(-3)+(+10)=12(cm).
(3)取所有路程的绝对值,得
|+5|+|3|+|+10|+|8|+|6|+|+12|+|10|
=5+3+10+8+6+12+10
=54(cm).
由于每爬行1cm,奖励一粒糖,所以蚂蚁一共得到芝麻的粒数为:54×1=54(粒).
答: 蚂蚁一共得到54粒糖.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5﹣(﹣3)+(﹣2)﹣1;
(2)2
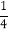 ×(﹣
×(﹣ )÷(﹣3);
)÷(﹣3);(3)﹣5×[1﹣(0.5+
 )÷
)÷ ];
];(4)20×(﹣
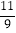 )+4×(﹣
)+4×(﹣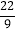 )+2×(﹣
)+2×(﹣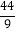 );
);(5)﹣14-(
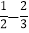 )÷(﹣
)÷(﹣ )×[﹣2﹣(﹣3)2]﹣(
)×[﹣2﹣(﹣3)2]﹣( ﹣0.52).
﹣0.52). -
科目: 来源: 题型:
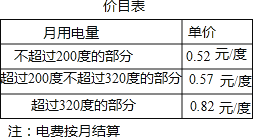
查看答案和解析>>【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
若某户居民1月份用电250度,则应收电费:0.52×200+0.57×(250﹣200)=132.5元.
(1)若某户居民10月份电费78元,则该户居民10月份用电_______度;
(2)若该户居民2月份用电340度,则应缴电费_______元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
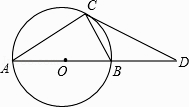
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解全校学生上学期参加“生涯规划”社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率
活动次数x
频数
频率
0<x≤3
10
0.20
3<x≤6
a
0.24
6<x≤9
16
0.32
9<x≤12
6
0.12
12<x≤15
b
m
15<x≤18
2
n
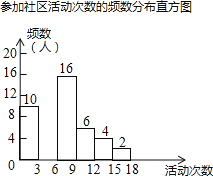
根据以上图表信息,解答下列问题:
(1)表中a= , b= , m= , n= .
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ 的图象上,直线AB经过点P(
的图象上,直线AB经过点P(  ,
,  ),求此抛物线的表达式.
),求此抛物线的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=6cm, ∠BAO=30°,点F为AB的中点.
(1)求OF的长度;
(2)求AC的长.

相关试题

