搜索
【题目】如图,已知△ABC和△A'B'C'关于直线m对称.
(1)结合图形指出对称点;
(2)若连接AA',直线m与线段AA'有什么关系?
(3)BC与B'C'的交点,AB与A'B'的交点分别与直线m有怎样的关系?若延长AC与A'C',其交点与直线m有怎样的关系?你发现了什么规律?
参考答案：
【答案】(1)A点的对称点是A',B点的对称点是B',C点的对称点是C'；(2)垂直平分；(3)延长线的交点都在直线m上.规律:成轴对称的两个三角形的对应线段(或其延长线)的交点在对称轴上.
【解析】
根据轴对称的性质即可得出答案．
(1)A点的对称点是A',B点的对称点是B',C点的对称点是C'.
(2)直线m垂直平分线段AA'.
(3)BC与B'C'的交点、AB与A'B'的交点、AC与A'C'的延长线的交点都在直线m上.规律:成轴对称的两个三角形的对应线段(或其延长线)的交点在对称轴上.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知二次函数图象的对称轴为直线x=2，顶点为点C，直线y=x+m与该二次函数的图象交于点A，B两点，其中点A的坐标为（5，8），点B在y轴上．
（1）求m的值和该二次函数的表达式．P为线段AB上一个动点（点P不与A，B两点重合），过点P作x轴的垂线，与这个二次函数的图象交于点E．
①设线段PE的长为h，求h与x之间的函数关系式，并写出自变量x的取值范围．
②若直线AB与这个二次函数图象的对称轴的交点为D，求当四边形DCEP是平行四边形时点P的坐标．
（2）若点P（x，y）为直线AB上的一个动点，试探究：以PB为直径的圆能否与坐标轴相切？如果能请求出点P的坐标，如果不能，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】点C为直线AB上一点,点M、N分别是线段AC、线段BC的中点。
(1)如图,若C为线段AB上一点,AC=6,BC=4,求线段MN的长；
(2)若C为线段AB上任一点,满足AC+BC=
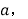其他条件不变,请直接写出线段MN的长(用含
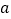的代数式表示)；(3)若C为线段AB的延长线上一点,且满足AC-BC=
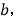其他条件不变,请直接写出线段MN的长(用含
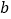的代数式表示)。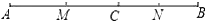
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在Rt△ABC和Rt△BCD中，∠ABC=∠BCD=90°，BD与AC相交于点E，AB=9，cos∠BAC=
，tan∠DBC= 
． 
求：
（1）边CD的长；
（2）△BCE的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】一辆货车从超市出发,向东走了3千米到达A地,继续向东走25千米到达B地,然后向西走了10千米到达C地,最后回到超市。
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,画出数轴并在数轴上表示出A地、B地、C地的位置；
(2)求C地距离A地多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.5升,这次共耗油多少升?
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解:
我们知道:一条线段有两个端点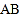，线段
和线段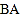
表示同一条线段. 若在直线
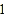上取了三个不同的点，则以它们为端点的线段共有 条;若取了四个不同的点，则共有线段 条;…;依此类推，取了
个不同的点，共有线段条.(用含的代数式表示)类比探究:
以一个锐角的顶点为端点向这个角的内部引射线.
(1)若引出两条射线，则所得图形中共有 个锐角;
(2)若引出
条射线，则所得图形中共有 个锐角.(用含的代数式表示)拓展应用:
一条铁路上共有8个火车站，若一列火车往返过程中必须停靠每个车站，则铁路局需为这条线路准备多少种车票?
-
科目： 来源： 题型：
查看答案和解析>>【题目】有两种包装盒，大盒比小盒可多装20克某一物品．已知120克这一物品单独装满小盒比单独装满大盒多1盒．
（1）问小盒每个可装这一物品多少克？
（2）现有装满这一物品两种盒子共50个．设小盒有n个，所有盒子所装物品的总量为w克． ①求w关于n的函数解析式，并写出定义域；
②如果小盒所装物品总量与大盒所装物品总量相同，求所有盒子所装物品的总量．
相关试题
