【题目】某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.设每户家庭用水量为x立方米时,应交水费y元.
(1)当![]() 时,y= (用含x的代数式表示);
时,y= (用含x的代数式表示);
当![]() 时,y= (用含x的代数式表示);
时,y= (用含x的代数式表示);
(2)小明家第二季度交纳水费的情况如下:
月份 | 四月份 | 五月份 | 六月份 |
交费金额 | 30元 | 34元 | 47.8元 |
小明家这个季度共用水多少立方米?
参考答案:
【答案】(1)y=2x;y=2.6x-12;(2)55立方米.
【解析】
(1)因为月用水量不超过20m3时,按2元/m3计费,
所以当0≤x≤20时,y与x的函数表达式是y=2x;
因为月用水量超过20m3时,其中的20m3仍按2元/m3收费,超过部分按2.6元/m3计费,
所以当x>20时,y与x的函数表达式是y=2×20+2.6(x-20),即y=2.6x-12;
(2)由题意可得:因为四月份、五月份缴费金额不超过40元,所以用y=2x计算用水量;六月份缴费金额超过40元,所以用y=2.6x-12计算用水量,
故2x=30,解得:x=15,即四月份用水15 m3,
2x=34,解得:x=17,即五月份用水17 m3,
2.6x-12=47.8,解得:x=23,即六月份用水23 m3,
15+17+23=55 m3,
∴小明家这个季度共用水55立方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量
单价
不超过
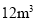 的部分
的部分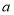 元/
元/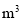
超过
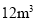 但不超过
但不超过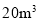 的部分
的部分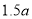 元/
元/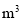
超过
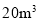 的部分
的部分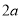 元/
元/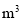
(1)当
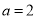 时,某用户一个月用了
时,某用户一个月用了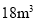 水,求该用户这个月应缴纳的水费;
水,求该用户这个月应缴纳的水费;(2)设某户月用水量为
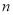 立方米,当
立方米,当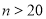 时,求该用户应缴纳的水费(用含
时,求该用户应缴纳的水费(用含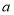 、
、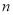 的整式表示);
的整式表示);(3)当
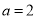 时,甲、乙两用户一个月共用水
时,甲、乙两用户一个月共用水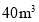 .已知甲用户用水量超过了
.已知甲用户用水量超过了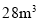 ,设甲用户这个月用水如
,设甲用户这个月用水如,试求甲、乙两用户一个月共缴纳的水费.(用含
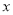 的整式表示)
的整式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】某型拖拉机油箱贮满油
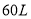 ,在正常情况下,拖拉机工作
,在正常情况下,拖拉机工作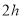 耗油
耗油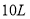 .
.(1)拖拉机每小时耗油______
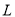 ;
;(2)工作
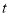 小时后油箱还剩油量为______
小时后油箱还剩油量为______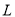 ;
;(3)当油箱中剩下
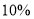 时,拖拉机停止工作,该型拖拉机加满一箱油最长工作多长时间?
时,拖拉机停止工作,该型拖拉机加满一箱油最长工作多长时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
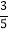 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
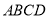 中,以点
中,以点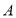 为圆心,
为圆心,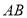 长为半径画弧交
长为半径画弧交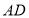 于点
于点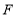 ,再分别以点
,再分别以点 为圆心,大于二分之一
为圆心,大于二分之一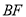 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点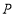 ,连接
,连接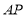 并延长交
并延长交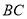 于点
于点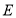 ,连接
,连接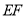 .
.(1)四边形
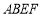 是__________; (填矩形、菱形、正方形或无法确定)
是__________; (填矩形、菱形、正方形或无法确定)(2)如图,
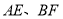 相交于点
相交于点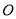 ,若四边形
,若四边形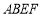 的周长为
的周长为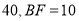 ,求
,求 的度数.
的度数.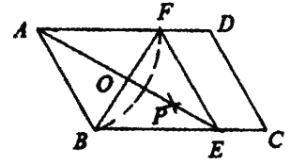
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为
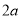 、宽为
、宽为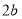 的长方形(其中
的长方形(其中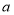 ,
,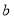 均为正数,且
均为正数,且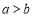 ),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.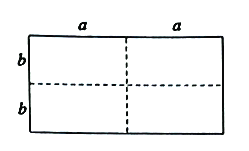
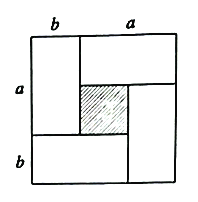
图1 图2
(1)图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含
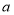 、
、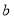 的代数式表示)
的代数式表示)(2)仔细观察图2,请你写出下列三个代数式:
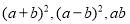 所表示的图形面积之间的相等关系,并选取适合
所表示的图形面积之间的相等关系,并选取适合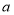 ,
,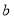 的数值加以验证.
的数值加以验证.(3)已知
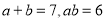 .则代数式
.则代数式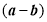 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点
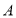 、点
、点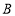 表示的数分别为
表示的数分别为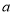 、
、 ,则
,则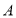 、
、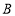 两点之间的距离
两点之间的距离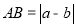 ,线段
,线段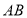 的中点表示的数为
的中点表示的数为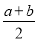 .
.(问题情境)
如图,数轴上点
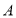 表示的数为
表示的数为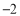 ,点
,点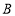 表示的数为8,点
表示的数为8,点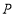 从点
从点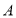 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点 从点
从点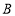 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为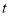 秒(
秒( ).
).(综合运用)
(1)填空:
①
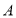 、
、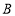 两点之间的距离
两点之间的距离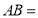 ________,线段
________,线段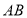 的中点表示的数为__________.
的中点表示的数为__________.②用含
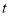 的代数式表示:
的代数式表示: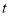 秒后,点
秒后,点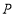 表示的数为____________;点
表示的数为____________;点 表示的数为___________.
表示的数为___________.③当
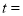 _________时,
_________时,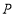 、
、 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.(2)当
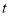 为何值时,
为何值时,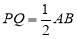 .
.(3)若点
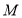 为
为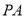 的中点,点
的中点,点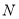 为
为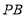 的中点,点
的中点,点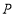 在运动过程中,线段
在运动过程中,线段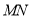 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段 的长.
的长.
相关试题

