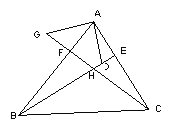
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何。
参考答案:
【答案】(1)证明见解析(2)位置关系是AD⊥GA,利用见解析.
【解析】
试题分析:(1)先根据条件证明△BHF∽△CHE得出∠ABD=∠ACG,然后可证△ABD≌△GCA,从而可得AD=AG;(2)根据△ABD≌△GCA得出∠ADB=∠GAC,然后利用角的关系得出∠AED=∠GAD=90°,即可得证.
试题解析:(1)∵BE⊥AC,CF⊥AB,
∴∠HFB=∠HEC=90°,又∠BHF=∠CHE,
∴△BHF∽△CHE,
∴∠ABD=∠ACG,
在△ABD和△GCA中
 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA(全等三角形的对应边相等);
(2)位置关系是AD⊥GA,
理由为:∵△ABD≌△GCA,
∴∠ADB=∠GAC,
又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,
∴∠AED=∠GAD=90°,
∴AD⊥GA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个以﹣3和2为根且二次项系数为1的一元二次方程________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为4和6,则它的周长等于_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读材料,再结合要求回答问题.
【问题情景】
如图①:在四边形ABCD中,AB=AD,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且线段BE,EF,FD满足BE+FD=EF.试探究图中∠EAF与∠BAD之间的数量关系.

【初步思考】
小王同学探究此问题的方法是:延长FD到G,使DG=BE,连结AG.
先证明△ABE≌△ADG,再证明△AEF≌△AGF,
可得出∠EAF与∠BAD之间的数量关系是 .
【探索延伸】
若将问题情景中条件“∠B=∠ADC=90°”改为“∠B+∠D=180°”(如图②),其余条件不变,请判断上述数量关系是否仍然成立,若成立,请证明;若不成立,请说明理由.
【实际应用】
如图③,在某次军事演习中,舰艇甲在指挥中心(O)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处且相距210海里.试求此时两舰艇的位置与指挥中心(O处)形成的夹角∠EOF的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
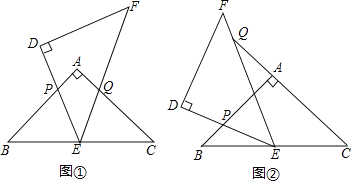
(1)如图①,当点Q在线段AC上,求证:△BPE∽△CEQ;
(2)如图①,当点Q在线段AC上,当AP=4,BP=8时,求P、Q两点间的距离;
(3)如图②,当点Q在线段CA的延长线上,若BP=2a,CQ=9a,求PE:EQ的值,并直接写出△EPQ的面积 (用含a的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
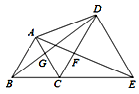
A.△ACE≌△BCD B.△BGC≌△AFC C.△DCG≌△ECF D.△ADB≌△CEA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.
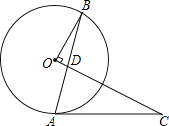
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OC=13,OD=1,求⊙O的半径及tanB.
相关试题

