【题目】已知f(x)=|x﹣a|,a∈R.
(1)当a=1时,求不等式f(x)+|2x﹣5|≥6的解集;
(2)若函数g(x)=f(x)﹣|x﹣3|的值域为A,且[﹣1,2]A,求a的取值范围.
参考答案:
【答案】
(1)解:a=1时,|x﹣1|+|2x﹣5|≥6,
x≤1时:1﹣x﹣2x+5≥6,解得:x≤0,∴x≤0,
1<x<2.5时:x﹣1﹣2x+5≥6,解得:x≤﹣1,不成立;
x≥2.5时:x﹣1+2x﹣5≥6,解得:x≥4,∴x≥4,
故不等式的解集是{x|x≥4或x≤0};
(2)解:g(x)=|x﹣a|﹣|x﹣3|,
a≥3时:g(x)=  ,
,
∴3﹣a≤g(x)≤a﹣3,
∵[﹣1,2]A,∴ ![]() ,解得a≥5;
,解得a≥5;
a<3时,a﹣3≤g(x)≤3﹣a,
∴ ![]() ,解得:a≤1;
,解得:a≤1;
综上:a≤1或a≥5
【解析】(1)将a=1代入f(x),通过讨论x的范围求出各个区间上的x的范围,取并集即可;(2)通过讨论a的范围,得到关于a的不等式组,解出即可.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线E:y2=4x的准线为l,焦点为F,O为坐标原点.
(1)求过点O,F,且与l相切的圆的方程;
(2)过F的直线交抛物线E于A,B两点,A关于x轴的对称点为A′,求证:直线A′B过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 x3﹣
x3﹣  x2+logax,(a>0且a≠1)为定义域上的增函数,f'(x)是函数f(x)的导数,且f'(x)的最小值小于等于0. (Ⅰ)求a的值;
x2+logax,(a>0且a≠1)为定义域上的增函数,f'(x)是函数f(x)的导数,且f'(x)的最小值小于等于0. (Ⅰ)求a的值;
(Ⅱ)设函数 ,且g(x1)+g(x2)=0,求证:
,且g(x1)+g(x2)=0,求证: 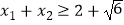 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xoy中,直线的参数方程为
 (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为 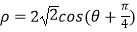 .
.
(1)求曲线C的直角坐标方程,并指出其表示何种曲线;
(2)设直线l与曲线C交于A,B两点,若点P的直角坐标为(1,0),试求当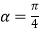 时,|PA|+|PB|的值.
时,|PA|+|PB|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=1+2cosxcos(x+3φ)是偶函数,其中φ∈(0,
 ),则下列关于函数g(x)=cos(2x﹣φ)的正确描述是( )
),则下列关于函数g(x)=cos(2x﹣φ)的正确描述是( )
A.g(x)在区间[﹣ ]上的最小值为﹣1.
]上的最小值为﹣1.
B.g(x)的图象可由函数f(x)向上平移2个单位,在向右平移 个单位得到.
个单位得到.
C.g(x)的图象可由函数f(x)的图象先向左平移 个单位得到.
个单位得到.
D.g(x)的图象可由函数f(x)的图象先向右平移 个单位得到.
个单位得到. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,F1 , F2分别是双曲线
 的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,
的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1, 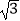 ),若△ABF2为等边三角形,则△BF1F2的面积为( )
),若△ABF2为等边三角形,则△BF1F2的面积为( ) 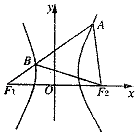
A.1
B.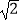
C.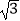
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,a2=
 .
.
(1)若数列{an}满足2an﹣an+1=0,求an;
(2)若a4= ,且数列{(2n﹣1)an+1}是等差数列,求数列{
,且数列{(2n﹣1)an+1}是等差数列,求数列{ 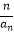 }的前n项和Tn .
}的前n项和Tn .
相关试题

