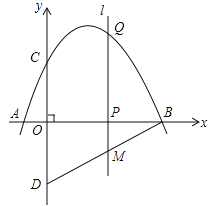
【题目】如图,抛物线![]() 与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A、点B、点C的坐标;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(4)在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)A(﹣1,0),B(4,0),C(0,2);(2)![]() ;(3)m=2;(4)Q的坐标为(3,2),(8,﹣18),(﹣1,0).
;(3)m=2;(4)Q的坐标为(3,2),(8,﹣18),(﹣1,0).
【解析】
试题分析:(1)根据函数解析式列方程即可得到结论;
(2)由点C与点D关于x轴对称,得到D(0,﹣2),解方程即可得到结论;
(3)如图1所示:根据平行四边形的性质得到QM=CD,设点Q的坐标为(m,![]() ),则M(m,
),则M(m,![]() ),列方程即可得到结论;
),列方程即可得到结论;
(4)设点Q的坐标为(m,![]() ),分两种情况:①当∠QBD=90°时,根据勾股定理列方程求得m=3,m=4(不合题意,舍去),②当∠QDB=90°时,根据勾股定理列方程求得m=8,m=﹣1,于是得到结论.
),分两种情况:①当∠QBD=90°时,根据勾股定理列方程求得m=3,m=4(不合题意,舍去),②当∠QDB=90°时,根据勾股定理列方程求得m=8,m=﹣1,于是得到结论.
试题解析:(1)∵令x=0得;y=2,∴C(0,2).
∵令y=0得:![]() ,解得:
,解得:![]() ,
,![]() ,∴A(﹣1,0),B(4,0).
,∴A(﹣1,0),B(4,0).
(2)∵点C与点D关于x轴对称,∴D(0,﹣2).
设直线BD的解析式为y=kx﹣2.
∵将(4,0)代入得:4k﹣2=0,∴k=![]() ,∴直线BD的解析式为
,∴直线BD的解析式为![]() .
.
(3)如图1所示:

∵QM∥DC,∴当QM=CD时,四边形CQMD是平行四边形.
设点Q的坐标为(m,![]() ),则M(m,
),则M(m,![]() ),∴
),∴![]() ,解得:m=2,m=0(不合题意,舍去),∴当m=2时,四边形CQMD是平行四边形;
,解得:m=2,m=0(不合题意,舍去),∴当m=2时,四边形CQMD是平行四边形;
(4)存在,设点Q的坐标为(m,![]() ),∵△BDQ是以BD为直角边的直角三角形,∴分两种情况讨论:
),∵△BDQ是以BD为直角边的直角三角形,∴分两种情况讨论:
①当∠QBD=90°时,由勾股定理得:![]() ,即
,即![]() ,解得:m=3,m=4(不合题意,舍去),∴Q(3,2);
,解得:m=3,m=4(不合题意,舍去),∴Q(3,2);
②当∠QDB=90°时,由勾股定理得:![]() ,即
,即![]() ,解得:m=8,m=﹣1,∴Q(8,﹣18),(﹣1,0);
,解得:m=8,m=﹣1,∴Q(8,﹣18),(﹣1,0);
综上所述:点Q的坐标为(3,2),(8,﹣18),(﹣1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边等于3,一边等于7,那么它的周长等于( )
A.17B.13C.13或15D.13或17
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年中秋小长假长沙县的旅游收入约为1900万,将1900万用科学记数法表示应为( )
A. 19×104 B. 1.9×104 C. 1.9×107 D. 0.19×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
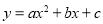 ( a≠0)经过原点,顶点为A ( h,k ) (h≠0).
( a≠0)经过原点,顶点为A ( h,k ) (h≠0).(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线
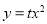 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;(3)当点A在抛物线
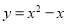 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个数是–5,另一个数比|–5|的相反数大4,则这两个数的积是( )
A. 6 B. –5 C. –6 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形、平行四边形、矩形、菱形、正方形、正五边形中,既是轴对称图形,又是中心对称图形的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题:①若a﹥b则a+b﹥0;②若a≠b则a2≠b2;③角的平分线上的点到角两边的距离相等;④平行四边形的对角线互相平分。其中原命题和逆命题都正确的个数是( )
A.1个
B.2个
C.3个
D.4个
相关试题

