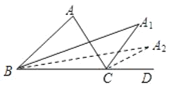
【题目】如图,在△ABC中,∠A=β度,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线交于点A2,得∠A2,…∠A2017BC与∠A2017CD的平分线交于点A2018,得∠A2018.则∠A2018=_____度.
参考答案:
【答案】![]()
【解析】
设∠ABC=2α,所以∠ACD=2α+β,由角平分线的性质可知∠A1CD=![]() ∠ACD=
∠ACD=![]() +α,∠A1BC=
+α,∠A1BC=![]() ∠ABC=α,由三角形的外角性质可知∠A1=
∠ABC=α,由三角形的外角性质可知∠A1=![]() ,同理可求出∠A2=
,同理可求出∠A2=![]() ,∠A3=
,∠A3=![]() ,根据规律即可求出∠A2018=
,根据规律即可求出∠A2018=![]() .
.
设∠ABC=2α,
∴∠ACD=2α+β,
∵∠ABC与∠ACD的平分线交于点A1
∴∠A1CD=![]() ∠ACD=
∠ACD=![]() +α,∠A1BC=
+α,∠A1BC=![]() ∠ABC=α,
∠ABC=α,
∵∠A1CD=∠A1BC+∠A1,
∴∠A1=![]()
同理可得:∠A2=![]() ,∠A3=
,∠A3=![]() ,
,
∴∠A2018=![]()
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.
(1)在这个过程中,自变量是 ,因变量是 .
(2)景点离小明家多远?
(3)小明一家在景点游玩的时间是多少小时?
(4)小明到家的时间是几点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
如图①,
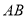 、
、 是⊙
是⊙ 的两条弦,
的两条弦,  ,
,  是
是 的中点,
的中点,  ,垂足为
,垂足为 .
.求证:
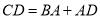 .
.

小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
如图②,延长
 至
至 ,使
,使 ,连接
,连接 、
、 、
、 、
、 、
、 .
.(请你在下面的空白处完成小敏的证明过程.)
推广运用
如图③,等边
 内接于⊙
内接于⊙ ,
,  .
.  是
是 上一点,
上一点,  ,
,  ,垂足为
,垂足为 ,则
,则 的周长是__________.
的周长是__________.

拓展研究
如图④,若将“问题提出”中的“
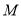 是
是 的中点”改成“
的中点”改成“ 是
是 的中点”,其余条件不变,“
的中点”,其余条件不变,“ ”这一结论还成立吗?若成立,请说明理由;若不成立,写出
”这一结论还成立吗?若成立,请说明理由;若不成立,写出 、
、 、
、 三者之间存在的关系并说明理由.
三者之间存在的关系并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=
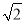 ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+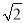 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+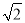 …按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
…按此规律继续旋转,直至得到点P2018为止,则AP2018为( )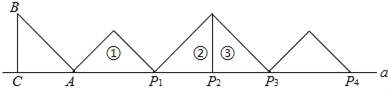
A. 1345+376
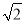 B. 2017+
B. 2017+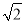 C. 2018+
C. 2018+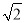 D. 1345+673
D. 1345+673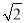
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②b<a﹣c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b),(m≠1的实数)⑥2a+b+c>0,其中正确的结论的有( )
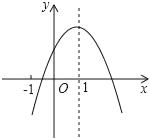
A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形
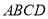 的对角线
的对角线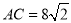 ,
,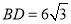 ,
,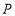 、
、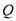 、
、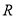 、
、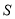 分别是
分别是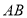 、
、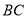 、
、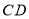 、
、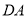 的中点,则
的中点,则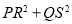 的值是_______.
的值是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达点B为止;点Q以2 cm/s的速度向点D移动。经过长时间P、Q两点之间的距离是10 cm?(8′)

相关试题

