【题目】已知四边形![]() 的对角线
的对角线![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点,则
的中点,则![]() 的值是_______.
的值是_______.
参考答案:
【答案】118
【解析】
先根据![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点得到四边形PQRS是平行四边形,再根据平行四边形的对角线的平方与四条边边长的平方的关系即可得到答案.
的中点得到四边形PQRS是平行四边形,再根据平行四边形的对角线的平方与四条边边长的平方的关系即可得到答案.
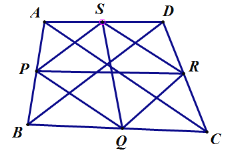
∵![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点,
的中点,
∴![]() =
=![]()
![]() (中位线的性质),
(中位线的性质),
同理可得:![]() =
=![]()
![]()
并且有 PS∥BD,PS=![]() BD(中位线的性质),
BD(中位线的性质),
同理可得:QR∥BD,QR=![]()
![]() ,
,
∴PS∥QR,![]() (等量替换),
(等量替换),
∴四边形PQRS是平行四边形,
∴![]() =
=![]() +
+![]() (平行四边形两条对角线的平方和等于四条边长的平方和,后附证明过程)
(平行四边形两条对角线的平方和等于四条边长的平方和,后附证明过程)
= ![]()
=27+32+27+32
=118.
附:四边形ABCD是平行四边形,则![]() =
=![]() +
+![]()
证明: 如图,作![]() 垂直
垂直![]() 于E,作
于E,作![]() 垂直于
垂直于![]() 的延长线,交于点F.
的延长线,交于点F.
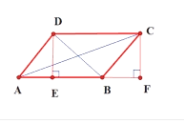
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD=BC,
∴DE=CF(两平行线间的距离相等),
∴Rt△AED≌Rt△BFC(HL)
∴AE=BF,
根据勾股定理得:
![]() ,
,
![]() ,
,
![]() ,
,
=![]()
=![]()
∵![]() (勾股定理)
(勾股定理)
∴![]() =
=![]() +
+![]() (等量替换).
(等量替换).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=
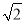 ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+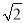 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+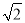 …按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
…按此规律继续旋转,直至得到点P2018为止,则AP2018为( )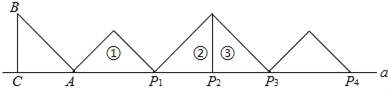
A. 1345+376
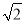 B. 2017+
B. 2017+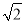 C. 2018+
C. 2018+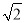 D. 1345+673
D. 1345+673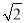
-
科目: 来源: 题型:
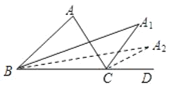
查看答案和解析>>【题目】如图,在△ABC中,∠A=β度,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线交于点A2,得∠A2,…∠A2017BC与∠A2017CD的平分线交于点A2018,得∠A2018.则∠A2018=_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②b<a﹣c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b),(m≠1的实数)⑥2a+b+c>0,其中正确的结论的有( )
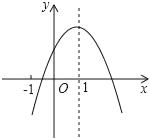
A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达点B为止;点Q以2 cm/s的速度向点D移动。经过长时间P、Q两点之间的距离是10 cm?(8′)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,BC=2AB,M是AD的中点,CE⊥AB,垂足为E,求证:∠DME=3∠AEM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
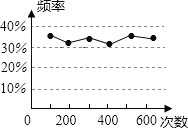
A. 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B. 掷一枚质地均匀的硬币,正面朝上的概率
C. 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D. 任意买一张电影票,座位号是2的倍数的概率
相关试题

