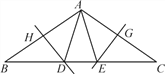
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
A. ![]() B. AD,AE将∠BAC三等分
B. AD,AE将∠BAC三等分
C. △ABE≌△ACD D. S△ADH=S△CEG
【答案】A
【解析】试题解析:∵∠B=∠C=36°,∴AB=AC,∠BAC=108°,∵DH垂直平分AB,EG垂直平分AC,∴DB=DA,EA=EC,∴∠B=∠DAB=∠C=∠CAE=36°,∴△BDA∽△BAC,∴![]() ,又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,∴∠ADC=∠DAC,∴CD=CA=BA,∴BD=BC﹣CD=BC﹣AB,则
,又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,∴∠ADC=∠DAC,∴CD=CA=BA,∴BD=BC﹣CD=BC﹣AB,则![]() =
=![]() ,即
,即![]() =
=![]() ,故A错误;
,故A错误;
∵∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,∴∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°,即∠DAB=∠DAE=∠CAE=36°,∴AD,AE将∠BAC三等分,故B正确;
∵∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,∴∠BAE=∠CAD,在△BAE和△CAD中,∵∠B=∠C,AB=AC,∠BAE=∠CAD,∴△BAE≌△CAD,故C正确;
由△BAE≌△CAD可得S△BAE=S△CAD,即S△BAD+S△ADE=S△CAE+S△ADE,∴S△BAD=S△CAE,又∵DH垂直平分AB,EG垂直平分AC,∴S△ADH=![]() S△ABD,S△CEG=
S△ABD,S△CEG=![]() S△CAE,∴S△ADH=S△CEG,故D正确.
S△CAE,∴S△ADH=S△CEG,故D正确.
故选A.
【题型】单选题
【结束】
11
【题目】红细胞是人体中血液运输氧气的主要媒介,人体中红细胞的直径约为0.0000077m,将0.0000077用科学记数法表示为 .
参考答案:
【答案】7.7×10-6.
【解析】
试题分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
试题解析:0.0000077用科学记数法表示为7.7×10-6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.
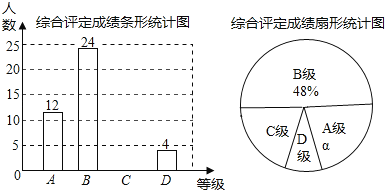
请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生;a= %;C级对应的圆心角为 度.
(2)补全条形统计图;
(3)若该校共有2000名学生,请你估计该校D级学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表给出三种上宽带网的收费方式.
收费方式
月使用费/元
包时上网时间/

超时费/(元/
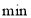 )
)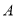

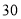
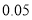
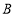
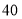
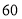
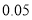
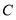
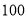
不限时
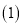 设月上网时间为
设月上网时间为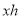 ,方式
,方式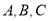 的收费金额分别为
的收费金额分别为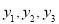 ,直接写出
,直接写出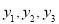 的解析式,并写出自变量
的解析式,并写出自变量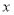 的取值范围;
的取值范围;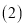 填空:
填空: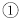 当上网时间 时,选择方式
当上网时间 时,选择方式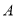 最省钱;
最省钱;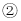 当上网时间 时,选择方式
当上网时间 时,选择方式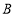 最省钱;
最省钱;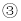 当上网时间 时,选择方式
当上网时间 时,选择方式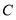 最省钱;
最省钱; -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x(
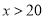 ).
).(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若
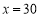 ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;(3)当
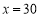 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用. -
科目: 来源: 题型:
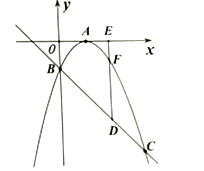
查看答案和解析>>【题目】如图,已知二次函数
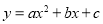 的图象顶点在
的图象顶点在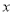 轴上,且
轴上,且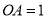 ,与一次函数
,与一次函数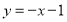 的图象交于
的图象交于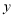 轴上一点
轴上一点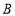 和另一交点
和另一交点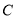 .
.
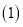 求抛物线的解析式;
求抛物线的解析式;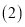 点
点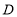 为线段
为线段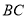 上一点,过点
上一点,过点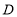 作
作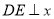 轴,垂足为
轴,垂足为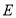 ,交抛物线于点
,交抛物线于点 ,请求出线段
,请求出线段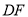 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
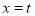 与直线
与直线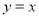 和直线
和直线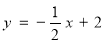 分别交于点
分别交于点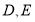 (
( 在
在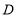 的上方).
的上方).
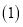 直线
直线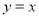 和直线
和直线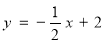 交于点
交于点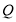 ,点
,点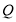 的坐标为 ;
的坐标为 ;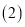 求线段
求线段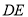 的长(用含
的长(用含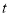 的代数式表示);
的代数式表示);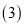 点
点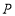 是
是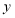 轴上一动点,且
轴上一动点,且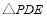 为等腰直角三角形,求
为等腰直角三角形,求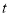 的值及点
的值及点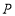 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形
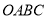 顶点
顶点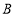 的坐标为
的坐标为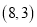 ,定点
,定点 的坐标为
的坐标为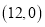 .动点
.动点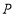 从点
从点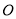 出发,以每秒
出发,以每秒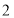 个单位长度的速度沿
个单位长度的速度沿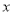 轴的正方向匀速运动,动点
轴的正方向匀速运动,动点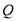 从点
从点 出发,以每秒
出发,以每秒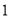 个单位长度的速度沿
个单位长度的速度沿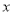 轴的负方向匀速运动,
轴的负方向匀速运动,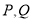 两点同时运动,相遇时停止.在运动过程中,以
两点同时运动,相遇时停止.在运动过程中,以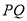 为斜边在轴上方作等腰直角三角形
为斜边在轴上方作等腰直角三角形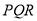 ,设运动时间为
,设运动时间为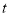 秒,
秒,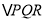 和矩形
和矩形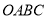 重叠部分的面积为
重叠部分的面积为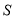 ,
,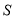 关于
关于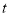 的函数如图2所示(其中
的函数如图2所示(其中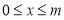 ,
,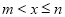 ,
, 时,函数的解析式不同).
时,函数的解析式不同).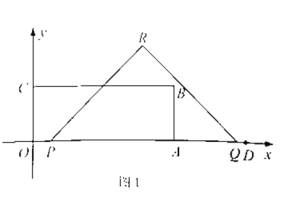

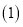 当
当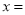 时,
时,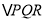 的边
的边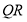 经过点
经过点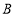 ;
;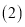 求
求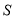 关于
关于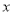 的函数解析式,并写出
的函数解析式,并写出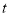 的取值范围.
的取值范围.
相关试题

