【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

参考答案:
【答案】(1) 25°;(2) ∠E=β-α
【解析】
(1)由∠B=35°,∠ACB=85°,根据三角形内角和等于180°,可得∠BAC的度数,因为AD平分∠BAC,从而可得∠DAC的度数,进而求得∠ADC的度数,由PE⊥AD,可得∠DPE的度数,从而求得∠E的度数.
(2)根据第一问的推导,可以用含α、β的代数式表示∠E.
(1)∵∠B=35°,∠ACB=85°,∴∠BAC=180°-∠B-∠ACB=60°.
∵AD平分∠BAC,∴∠DAC=∠BAD=30°.
∴∠ADC=∠B+∠BAD=65°.
又∵PE⊥AD,∴∠DPE=90°,
∴∠E=90°-∠ADC=25°.
(2)∵∠B=α,∠ACB=β,∴∠BAC=180°-α-β.
∵AD平分∠BAC,∴∠DAC=∠BAD=(180°-α-β).
∴∠ADE=∠B+∠BAD=90°+α-β,
又∵PE⊥AD,∴∠DPE=90°,
∴∠E=90°-∠ADE=β-α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB',FD′相交于点O.

简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是__________________.
(2)请你结合图1写出一条完美筝形的性质_______________.
(3)当图3中的∠BCD=120°时,∠AEB′=_________________.
(4)当图2中的四边形AECF为菱形时,对应图③中的“完美筝形”有__________________________(写出筝形的名称:例 筝形ABCD).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
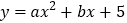 与
与 轴交于
轴交于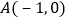 、
、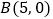 两点,直线
两点,直线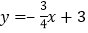 与
与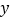 轴交于点
轴交于点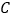 ,与
,与 轴交于点
轴交于点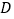 .点
.点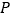 是抛物线上一动点,过点
是抛物线上一动点,过点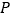 作直线
作直线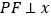 轴于点
轴于点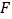 ,交直线
,交直线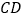 于点
于点 .设点
.设点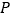 的横坐标为
的横坐标为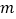 .
.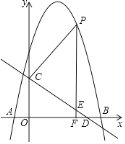
 求抛物线的解析式;
求抛物线的解析式; 若点
若点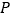 在
在 轴上方的抛物线上,当
轴上方的抛物线上,当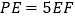 时,求点
时,求点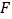 的坐标;
的坐标;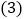 若点
若点 ’是点
’是点 关于直线
关于直线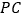 的对称点,当点
的对称点,当点 ’落在
’落在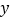 轴上时,请直接写出
轴上时,请直接写出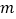 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
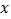 的二次方程
的二次方程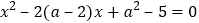 的两根为
的两根为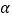 、
、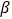 ,且
,且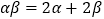 ,则
,则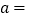 ________,
________,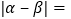 ________.
________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中, ,
, ,点
,点 从
从 开始沿折线
开始沿折线 以
以 的速度运动,点
的速度运动,点 从
从 开始沿
开始沿 边以
边以 的速度移动,如果点
的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为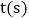 ,当
,当 ________时,四边形
________时,四边形 也为矩形.
也为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.

相关试题

