【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
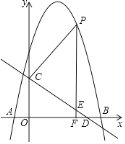
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 在
在![]() 轴上方的抛物线上,当
轴上方的抛物线上,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 若点
若点![]() ’是点
’是点![]() 关于直线
关于直线![]() 的对称点,当点
的对称点,当点![]() ’落在
’落在![]() 轴上时,请直接写出
轴上时,请直接写出![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)m的值为
;(3)m的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求出抛物线的解析式;
(2)用含m的代数式分别表示出PE、EF,然后列方程求解;
(3)解题关键是识别出当四边形PECE′是菱形,然后根据PE=CE的条件,列出方程求解;当四边形PECE′是菱形不存在时,P点y轴上,即可得到m的值.
解:![]() ∵抛物线
∵抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,
两点,
∴![]() ,
,
解得![]() ,
,
∴抛物线的解析式为![]() .
.
![]() ∵点
∵点![]() 的横坐标为
的横坐标为![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
![]() .
.
由题意,![]() ,即:
,即:![]()
①若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() .
.
由题意,![]() 的取值范围为:
的取值范围为:![]() ,故
,故![]() 、
、![]() 这两个解均舍去.
这两个解均舍去.
∴![]() 或
或![]() .
.
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
![]() 假设存在.
假设存在.
作出示意图如下:
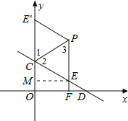
∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() ,
,![]() ,
,![]() .
.
∵![]() 平行于
平行于![]() 轴,∴
轴,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即四边形
,即四边形![]() 是菱形.
是菱形.
当四边形![]() 是菱形存在时,
是菱形存在时,
由直线![]() 解析式
解析式![]() ,可得
,可得![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() .
.
过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,易得
,易得![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() ,又由
,又由![]() 可知:
可知:![]()
∴![]() .
.
①若![]() ,整理得:
,整理得:![]() ,解得
,解得![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,解得
,解得![]() ,
,![]() .
.
由题意,![]() 的取值范围为:
的取值范围为:![]() ,故
,故![]() 这个解舍去.
这个解舍去.
当四边形![]() 是菱形这一条件不存在时,
是菱形这一条件不存在时,
此时![]() 点横坐标为
点横坐标为![]() ,
,![]() ,
,![]() ,
,![]() 三点重合与
三点重合与![]() 轴上,也符合题意,
轴上,也符合题意,
∴![]() ,
,
综上所述,存在满足条件的![]() 的值为
的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要建一个如图所示的面积为300
 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
(1)求围栏的长和宽;
(2)能否围成面积为400
 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB',FD′相交于点O.

简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是__________________.
(2)请你结合图1写出一条完美筝形的性质_______________.
(3)当图3中的∠BCD=120°时,∠AEB′=_________________.
(4)当图2中的四边形AECF为菱形时,对应图③中的“完美筝形”有__________________________(写出筝形的名称:例 筝形ABCD).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
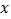 的二次方程
的二次方程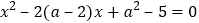 的两根为
的两根为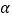 、
、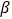 ,且
,且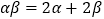 ,则
,则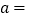 ________,
________,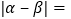 ________.
________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中, ,
, ,点
,点 从
从 开始沿折线
开始沿折线 以
以 的速度运动,点
的速度运动,点 从
从 开始沿
开始沿 边以
边以 的速度移动,如果点
的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为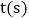 ,当
,当 ________时,四边形
________时,四边形 也为矩形.
也为矩形.
相关试题

