【题目】如图,在真角坐标系中,矩形0ABC的顶点A,C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N.
(1)求直线DE的函数表达式和点M,N的坐标;
(2)若函数y=![]() (k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(3)求△OMN的面积S;
(4)若函教y=![]() (k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.
(k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.

参考答案:
【答案】(1)y=-![]() x+3,M(2,2),N(4,1);
x+3,M(2,2),N(4,1);
(2)y=![]() ,点N在反比例函数图象上;
,点N在反比例函数图象上;
(3)3;
(4)k<0或0<k<4或k>8.
【解析】试题分析:(1)利用待定系数法即可求得直线DE的解析式,然后根据M的纵坐标是2,N的横坐标是4,即可求得M、N的坐标;
(2)利用待定系数即可求得反比例函数的解析式,然后把N的坐标代入解析式检验即可判断是否在反比例函数的图象上;
(3)根据△OMN的面积S=S梯形OCBM﹣S△OCN﹣S△BMN即可求解;
(4)根据经过M、N的反比例的函数的解析式,以及经过B的反比例函数的解析式,即可直接写出k的范围.
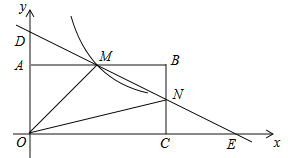
试题解析:解:(1)设直线DE的解析式是y=kx+b,根据题意得: ![]() ,解得:
,解得: 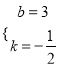 ,则直线DE的解析式是:y=﹣
,则直线DE的解析式是:y=﹣![]() x+3,令y=2,得到2=﹣
x+3,令y=2,得到2=﹣![]() x+3,解得:x=2,则M的坐标是(2,2),令x=4,解得:x=﹣2+3=1,则N的坐标是(4,1);
x+3,解得:x=2,则M的坐标是(2,2),令x=4,解得:x=﹣2+3=1,则N的坐标是(4,1);
(2)把(2,2)代入![]() 得;k=4,则反比例函数的解析式是:
得;k=4,则反比例函数的解析式是: ![]() ,当x=4时,y=1,则N在
,当x=4时,y=1,则N在![]() 的图象上;
的图象上;
(3)S梯形OCBM=![]() (BM+OC)BC=
(BM+OC)BC=![]() (2+4)2=6,S△OCN=
(2+4)2=6,S△OCN=![]() OCCN=
OCCN=![]() ×4×1=2,S△BMN=
×4×1=2,S△BMN=![]() BNBM=
BNBM=![]() ×1×2=1,则△OMN的面积S=6﹣2﹣1=3;
×1×2=1,则△OMN的面积S=6﹣2﹣1=3;
(4)经过M的反比例函数的解析式是: ![]() ,同时经过点N,则当0<k<4时,函数与△BNM没有交点;
,同时经过点N,则当0<k<4时,函数与△BNM没有交点;
经过点B的反比例函数的解析式是: ![]() ,则当k>8时,函数与△BMN没有交点;
,则当k>8时,函数与△BMN没有交点;
当k<0时,函数图象在二、四象限,则与△BMN没有交点.
故k的范围是:0<k<4或k>8或k<0.
-
科目: 来源: 题型:
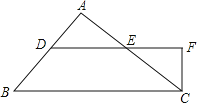
查看答案和解析>>【题目】如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于( )

A.90° B.75° C.70° D.60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,E的线段AD(除去端点A、D)上一动点,EF⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,求∠C的度数.
(2)当E在AD上移动时,∠B、∠C、∠DEF之间存在怎样的等量关系?请写出这个等量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠A=90°,点D、E分别在AB、AC上,DE∥BC,CF与DE的延长线垂直,垂足为F.
(1)求证:∠B=∠ECF ;
(2)若∠B=55°,求∠CED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,过点
中,过点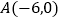 的直线
的直线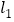 与直线
与直线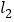 ;
;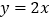 相交于点
相交于点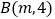 .
.(
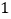 )求直线
)求直线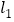 的表达式.
的表达式.(
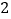 )过动点
)过动点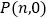 且垂于
且垂于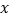 轴的直线与
轴的直线与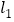 、
、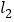 的交点分别为
的交点分别为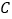 ,
,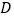 ,当点
,当点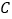 位于点
位于点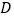 上方时,写出
上方时,写出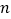 的取值范围.
的取值范围.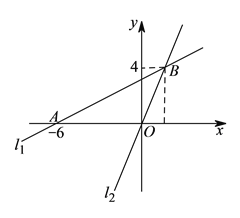
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市公交快速通道开通后,为响应市政府“绿色出行”的号召,家住新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的
 .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是张阳离家的距离与时间的关系图象.
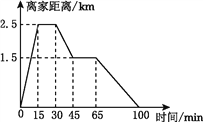
根据图象回答下列问题:
(1)体育场离张阳家多少千米?
(2)体育场离文具店多少千米?张阳在文具店逗留了多长时间?
(3)张阳从文具店到家的速度是多少?
相关试题

