Question

【题目】在△ABC中，AB=AC，点D是直线BC上一动点（不与点B，C重合），在AD右侧作△ADE，使得AD=AE，∠DAE=∠BAC，联结DE，CE。

（1）当点D在BC边上时，求证：EC=DB；

（2）当EC∥AB，若△ABD的最小角为20°，请写出ADB的度数，并对其中一个答案加以证明。

答：∠ADB的度数除了20°，还可能是 （直接写出所有答案，并对其中一个答案加以证明）

Answer 1

【答案】（1）见解析；（2）100°或40°．证明见解析

【解析】

（1）根据SAS证明△BAD≌△CAE，即可解答；
（2）分D在线段BC上、当点D在CB的延长线上、点D在BC的延长线上三种情形根据等边三角形的性质、三角形内角和定理计算即可．

（1）证明：如图，∵∠DAE=∠BAC，

∴∠BAD=∠CAE，
在△BAD和△CAE中，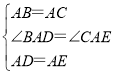
，
∴△BAD≌△CAE，

∴EC=DB.

（2）当D在线段BC上时，∵CE∥AB，
∴∠ACE=∠BAC，
∵△BAD≌△CAE，
∴∠ABD=∠ACE，

∴∠ABC=∠BAC，又∠ABC=∠ACB，
∴△ABC为等边三角形，
∴∠ABC=60°，
∴∠ADB=180°-60°-20°=100°；
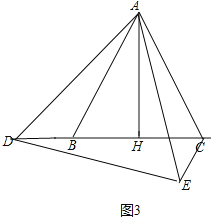
如图3，当点D在CB的延长线上时，同理可得，∠ABC=60°，
∴∠ADB=40°；
当点D在BC的延长线上时，只能∠ADB=20°，
∴∠ADB的度数为100°或40°或20°．