【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论: ①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】D
【解析】试题分析:①利用等边对等角,即可证得∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此可以求解;②证明∠POC=60°,且OP=OC,即可证得△OPC是等边三角形;③首先证明,△POA≌△CPE,则AO=CE,AC=AE+CE=AO+AP;④过带你C做CH⊥AB于H,根据S四边形AOCP=S△ACP+S△AOC,利用三角形的面积公式即可求解.所以4个结论都正确.
故选D.
-
科目: 来源: 题型:
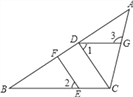
查看答案和解析>>【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a-2)0=1,则a的取值范围是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
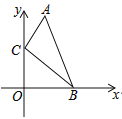
A. (0,0); B. (0,1); C. (0,2); D. (0,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,记录球的颜色,放回盒中,然后重复上述过程。
活动结果:摸球实验活动一共做了50次,统计结果如下表:

推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是年平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
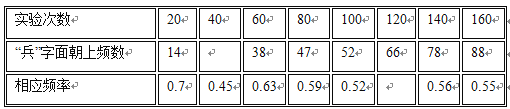
(1)请将数据补充完整;
(2)画出“兵”字面朝上的频率分布折线图;
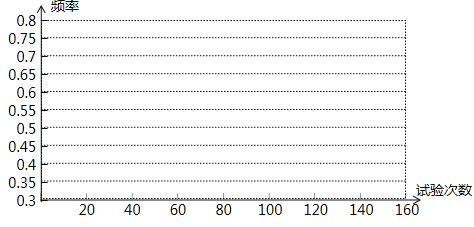
(3)如果实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由边长为1个单位长度的小正方形组成的网格图.
(1)请在图中建立平面直角坐标系,使A、B两点的坐标分别为A(2,3)、B(-2,0);
(2)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图中画出格点△ABC使得AB=AC,请写出在(1)中所建坐标系内所有满足条件的点C的坐标.

相关试题

