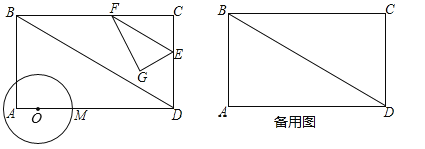
【题目】如图1,已知:在矩形ABCD中,AB![]() cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以
cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以![]() cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
(1)求a的值;
(2)在运动过程中,
①当直线FG与⊙O相切时,求t的值;
②是否存在某一时刻t,使点G恰好落在⊙O上(异于点M)?若存在,请直接写出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)a=2cm/s;(2)①t=![]() s或
s或![]() s时,直线FG与⊙O相切;②t=
s时,直线FG与⊙O相切;②t=![]() s时,点G在⊙O上.
s时,点G在⊙O上.
【解析】
(1)如图1中,当点G在AD上时,首先证明∠FEC=∠FEG=∠GED=60°,由EC=EG=![]() t,DE=
t,DE=![]() t,可得
t,可得![]() t+
t+![]() t=3
t=3![]() ,解方程即可;
,解方程即可;
(2)①如图2中,作GQ⊥AD于Q,GR⊥CD于R,QG的延长线交BC于P,FG的延长线交AD于T,解直角三角形求出TD,然后分情况讨论,分别列出方程求出相切时的时间;
②如图5中,作GN⊥AD,则DN=![]() t,ON=DN-OD=
t,ON=DN-OD=![]() t-(9-2t)=
t-(9-2t)=![]() t-9,NG=
t-9,NG=![]() ,OG=2,根据OG2=ON2+NG2,构建方程即可.
,OG=2,根据OG2=ON2+NG2,构建方程即可.
解:(1)如图1中,当点G在AD上时.
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AB=3![]() ,AD=9,
,AD=9,
∴tan∠BDA=![]() ,
,
∴∠ADB=30°,
∵BC∥AD,EF∥BD,
∴∠CFE=∠CBD=∠ADB=30°,
∴∠FEC=∠FEG=60°,
∴∠GED=60°,
∵CE=EG=![]() t,
t,
在Rt△GED中,DE=![]() t,
t,
∴![]() t+
t+![]() t=3
t=3![]() ,
,
∴t=2,
∴CE=EG=2![]() ,DE=
,DE=![]() ,DG=3,AG=6,
,DG=3,AG=6,
∵在整过移动过程中△EFG的直角顶点G能与点M重合,
∴2a+2=6,
∴a=2cm/s.
(2)①如图2中,作GQ⊥AD于Q,GR⊥CD于R,QG的延长线交BC于P,FG的延长线交AD于T.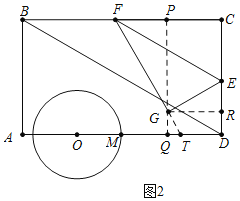
由题意CE=EG=![]() t,ER=
t,ER=![]() t,QD=PC=RG=
t,QD=PC=RG=![]() t,QG=DR=3
t,QG=DR=3![]() -
-![]() t-
t-![]() t=3
t=3![]() -
-![]() t,
t,
在Rt△GQT中,∵∠TGQ=30°,
∴QT=QGtan30°=3-![]() t,
t,
∴TD=![]() t-(3-
t-(3-![]() t)=3t-3,
t)=3t-3,
如图3中,当⊙O与FG相切于点N时,易知OA=2t,OT=![]() ,TD=3t-3,
,TD=3t-3,
则有2t+![]() +3t-3=9,
+3t-3=9,
解得t=![]() .
.
如图4中,当⊙O再次与FG相切时.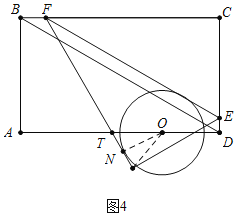
由OA+DT-OT=AD,可得2t+3t-3-![]() =9,
=9,
解得t=![]()
综上所述,t=![]() s或
s或![]() s时,直线FG与⊙O相切
s时,直线FG与⊙O相切
②如图5中,当点G在⊙O上时,
作GN⊥AD,则DN=![]() t,ON=DN-OD=
t,ON=DN-OD=![]() t-(9-2t)=
t-(9-2t)=![]() t-9,NG=
t-9,NG=![]() ,OG=2,
,OG=2,
∵OG2=ON2+NG2,
∴(![]() t-9)2+(
t-9)2+(![]() )2=4,
)2=4,
整理得:19t2-90t+104=0
∴(t-2)(19t-52)=0,
∴t=![]() 或t=2(舍弃)
或t=2(舍弃)
∴t=![]() s时,点G在⊙O上.
s时,点G在⊙O上.
-
科目: 来源: 题型:
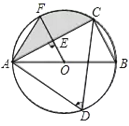
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°,且AB=6,过O点作OE⊥AC,垂足为E.
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积.(结果精确到0.01)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数图象与x轴,y轴分别交于点A(8,0),B(0,4),点C的坐标为(3,0),动点D是射线BO上一个动点,连结CD,过点C作CD⊥FC,交一次函数图象于点F.
(1)求这个一次函数的解析式;
(2)过点F作FE⊥x轴,垂足为点E,当△OCD与△EFC全等时,求出满足条件的点F的坐标;
(3)点D在运动过程中,是否存在使△ACF是等腰三角形?若存在请求出点F的坐标;不存在,请说明理由.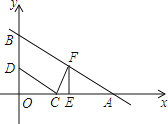
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
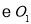 ,
,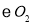 ,
,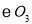 是等圆,
是等圆,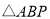 内接于
内接于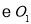 ,点
,点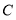 ,
,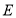 分别在
分别在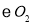 ,
,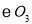 上.如图,
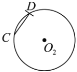
上.如图,①以
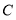 为圆心,
为圆心,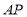 长为半径作弧交
长为半径作弧交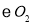 于点
于点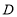 ,连接
,连接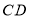 ;
;②以
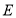 为圆心,
为圆心,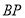 长为半径作弧交
长为半径作弧交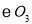 于点
于点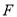 ,连接
,连接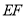 ;
;下面有四个结论:
①

②
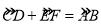
③
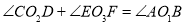
④
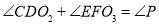
所有正确结论的序号是( ).
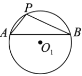
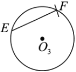
A.①②③④B.①②③C.②④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】改革开放40年以来,城乡居民生活水平持续快速提升.居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出.下图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图:
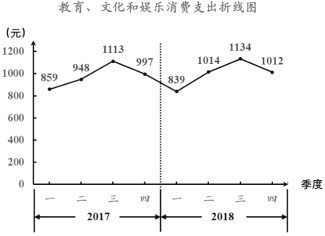
说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较.
根据上述信息,下列结论中错误的是( ).
A.2017年第二季度环比有所提高B.2017年第四季度环比有所下降
C.2018年第一季度同比有所提高D.2017和2018年支出最高的都是第三季度
相关试题

