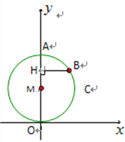
【题目】如图8,在平面直角坐标系中,点A坐标为(0,3),点B(![]() ,
,![]() )是以OA为直径的⊙M上的一点,且tan∠AOB=
)是以OA为直径的⊙M上的一点,且tan∠AOB=![]() ,BH⊥
,BH⊥![]() 轴,H为垂足,点C(
轴,H为垂足,点C(![]() ,
,![]() ).
).
(1)求H点的坐标;
(2)求直线BC的解析式;
(3)直线BC是否与⊙M相切?请说明理由.
参考答案:
【答案】(1) H(0,![]() ); (2)
); (2) ![]() =-
=-![]()
![]() +4;(3)见解析.
+4;(3)见解析.
【解析】分析:
(1)由已知易得tan∠AOB=![]() ,BH=
,BH=![]() ,由此即可解得m=
,由此即可解得m=![]() ,从而可得点H的坐标;
,从而可得点H的坐标;
(2)由(1)可知点B的坐标为![]() 结合点C的坐标即可由待定系数法求得直线BC的解析式;
结合点C的坐标即可由待定系数法求得直线BC的解析式;
(3)设直线BC与两坐标轴的交点分别为E、F,由(2)中所得解析式可求得点E、F的坐标,过点M作MN⊥BC于点N,由S△FME=![]() EF·MN=
EF·MN=![]() FM·EO,可证得MN的长等于⊙M的半径,由此即可得到BC是⊙M的切线.
FM·EO,可证得MN的长等于⊙M的半径,由此即可得到BC是⊙M的切线.
详解:
(1)由tan∠AOB=![]() ,得
,得![]() =
=![]() ,
,
∴OH=2BH,又B(![]() ,
,![]() ),即
),即![]() =2×
=2×![]() =
=![]() ,
,
∴H点的坐标为H(0,![]() );
);
(2)设过点B(![]() ,
,![]() )及点C(
)及点C(![]() ,
,![]() )
)
的直线解析式为:![]() =
=![]() +
+![]() ,
,
把BC坐标分别代入,得: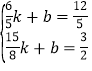 ,
,
解得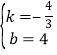 ,
,
∴直线BC的解析式为:![]() =-
=-![]()
![]() +4;
+4;
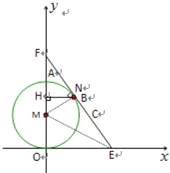
(3)BC与⊙M相切,理由如下
如下图,设直线BC:![]() 分别与
分别与![]() 轴
轴![]() 轴交于点EF,
轴交于点EF,
则点E的坐标为(3,0)点F的坐标为(0,4),
∴OE=3,OF=4,
∴EF=5,
过圆心M作MN⊥EF,垂足为N,连结ME,
∵S△FME=![]() EF·MN=
EF·MN=![]() FM·EO,
FM·EO,
∴得EF·MN=FM·EO,
∵⊙M的直径为3,
∴⊙M的半径OM=1.5,
∴MF=4-1.5=2.5,
∴MN=![]() =
=![]() ,
,
即圆心M到直线BC的距离等于⊙M的半径,
∴直线BC是⊙M的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭
 出发,晚上停留在
出发,晚上停留在 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):+5,-8,+10,-12,+6,-18,+5,-2.
(1)
 处在岗亭
处在岗亭 的什么方向?距离岗亭
的什么方向?距离岗亭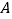 多远?
多远?(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若有理数a,b满足等式
 ,则称a,b是“雉水有理数对”,记作
,则称a,b是“雉水有理数对”,记作 如:数对
如:数对 ,
, 都是“雉水有理数对”.
都是“雉水有理数对”.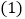 数对
数对 ______
______ 填“是”或“不是”
填“是”或“不是” “雉水有理数对”;
“雉水有理数对”; 若
若 是“雉水有理数对”,求m的值;
是“雉水有理数对”,求m的值; 请写出一个符合条件的“锥水有理数对”______
请写出一个符合条件的“锥水有理数对”______ 注意:不能与题目中已有的“雉水有理数对”重复
注意:不能与题目中已有的“雉水有理数对”重复
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.

(1)若∠AOC= 50°,则∠DOE= °;
(2)当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?
(3)图中与∠COD互补角的个数随∠AOC的度数变化而变化,直接写出与∠COD互补的角的个数及对应的∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是Rt△ABC斜边BC上的高.
(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);
(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;
(3)在(2)的条件下,连结DEDH.求证:ED⊥HD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
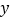 =
=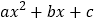 (
(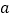 ≠0)与
≠0)与 轴交于AB两点,与
轴交于AB两点,与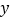 轴交于C点,其对称轴为
轴交于C点,其对称轴为 =1,且A(-1,0)C(0,2).
=1,且A(-1,0)C(0,2).(1)直接写出该抛物线的解析式;
(2)P是对称轴上一点,△PAC的周长存在最大值还是最小值?请求出取得最值(最大值或最小值)时点P的坐标;
(3)设对称轴与
 轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交
轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交 轴于点E.连接PDPE.若CD的长为
轴于点E.连接PDPE.若CD的长为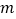 ,△PDE的面积为S,求S与
,△PDE的面积为S,求S与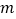 之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时
之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时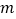 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

