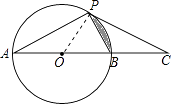
【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°. 
(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OP,如图所示:
∵PA=PC,∠C=30°,
∴∠A=∠C=30°,
∴∠APC=120°,
∵OA=OP,
∴∠OPA=∠A=30°,
∴∠OPC=120°﹣30°=90°,
即OP⊥CP,
∴CP是⊙O的切线.
(2)解:∵AB是⊙O的直径,
∴∠APB=90°,
∴∠OBP=90°﹣∠A=60°,
∵OP=OB=4,
∴△OBP是等边三角形,
∴阴影部分的面积=扇形OBP的面积﹣△OBP的面积= ![]() ﹣
﹣ ![]() ×4×2
×4×2 ![]() =
= ![]() ﹣4
﹣4 ![]() .
.
【解析】(1)连接OP,由等腰三角形的性质得出∠C=∠OPA=30°,∠APC=120°,求出∠OPC=90°即可;(2)证明△OBP是等边三角形,阴影部分的面积=扇形OBP的面积﹣△OBP的面积,即可得出结果.本题考查的是切线的判定、等腰三角形的性质、圆周角定理、等边三角形的判定与性质、扇形面积公式等知识;熟练掌握切线的判定.证明三角形是等边三角形是解决问题(2)的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,DE是过点A的直线,
,DE是过点A的直线, 于点D,
于点D, 于点E,
于点E, .
. 若BC在DE的同侧
若BC在DE的同侧 如图
如图 求证:
求证: .
. 若BC在DE的两侧
若BC在DE的两侧 如图
如图 ,其他条件不变,
,其他条件不变, 中的结论还成立吗?
中的结论还成立吗? 不需证明
不需证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:关于三角函数还有如下的公式:
sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)=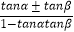
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan75°=tan(45°+30°)= =
=  =2+
=2+ 
根据以上阅读材料,请选择适当的公式解答下面问题
(1)计算:sin15°;
(2)某校在开展爱国主义教育活动中,来到烈士纪念碑前缅怀和纪念为国捐躯的红军战士.李三同学想用所学知识来测量如图纪念碑的高度.已知李三站在离纪念碑底7米的C处,在D点测得纪念碑碑顶的仰角为75°,DC为 米,请你帮助李三求出纪念碑的高度.
米,请你帮助李三求出纪念碑的高度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )

A. 3 B. 4 C. 3.5 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P,Q分别是边长为4 cm的等边三角形ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1 cm/s,连接AQ,CP,相交于点M.下面四个结论正确的有________(填序号).①BP=CM; ②△ABQ ≌△CAP ;③∠CMQ的度数不变,始终等于60;④当第
 s或
s或 s时,△PBQ为直角三角形.
s时,△PBQ为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴交于点C.

(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3)点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
相关试题

