【题目】一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:
(1)观察表中数据规律填表:
餐桌张数 | 1 | 2 | 3 | 4 | …n |
可坐人数 | 6 | 8 | 10 |
(2)一家酒楼,按上图的方式拼桌,要使拼成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
(3)若酒店有240人来就餐,哪种拼桌的方式更好?最少要用多少张餐桌?
参考答案:
【答案】
(1)解:
餐桌张数 | 1 | 2 | 3 | 4 | …n |
可坐人数 | 6 | 8 | 10 | 12 | 2n+4 |
(2)解:根据题意有:2n+4=160,
移项得:2n=160﹣4,2n=156,
n=78,需78张餐桌拼成一张刚好坐160人的大餐桌
(3)解:如果按本题给出的拼桌的方式,
由2n+4=240,解得n=118,
需118张餐桌拼成一张刚好坐240人的大餐桌.
如果按下列拼桌的方式,则有4n+2=240,解得n=59.5≈60
只需60张餐桌拼成一张能坐240人的大餐桌
【解析】(1)观察餐桌和椅子的摆放方式,可知每多放一张餐桌,就多坐2人,由此n张餐桌拼在一起可以坐2n+4个人。
(2) 根据(1)的结论建立方程,解方程求出n的值即可。
(3)若按本题给出的拼桌的方式,根据(1)的结论建立方程,解方程求出n的值;若按上图拼,可知每多放一张餐桌,就多坐4人,由此n张餐桌拼在一起可以坐4n+2个人,建立方程,解方程求出n的值(n为整数),比较大小即可得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列四组条件中,能判定ABCD是正方形的有( )
①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.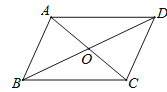
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2,照此规律作下去,则S1=_______,S2017=____________.
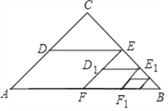
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正方形的面积是4cm2 , 则它的对角线长是( )
A.4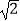 cm
cm
B.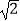 cm
cm
C.8cm
D.2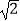 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )
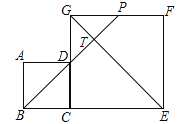
A.2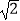
B.3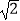
C.4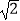
D.6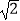
-
科目: 来源: 题型:
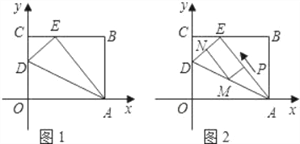
查看答案和解析>>【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
相关试题

