【题目】若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是_____.
参考答案:
【答案】m≤﹣![]() 或m≥﹣
或m≥﹣![]() .
.
【解析】解:设关于x的三个方程都没有实根.
对于方程x2+4mx+4m2+2m+3=0,则有△1<0,即△1=16m2﹣4(4m2+2m+3)<0,解得:m>﹣![]() ;
;
对于方程x2+(2m+1)x+m2=0,则有△2<0,即△2=(2m+1)2﹣4m2=4m+1<0,解得:m<﹣![]() ;
;
对于方程(m﹣1)x2+2mx+m﹣1=0,当m=1时,方程变为2x=0,方程有解,所以m≠1,则有△3<0,即△3=4m2﹣4(m﹣1)2=8m+4<0,解得:m<![]() .
.
综合所得:当﹣![]() <m<﹣
<m<﹣![]() ,且m≠1时,关于x的三个方程都没有实根.
,且m≠1时,关于x的三个方程都没有实根.
所以若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是 m≤﹣![]() 或m≥﹣
或m≥﹣![]() .
.
故答案为:m≤﹣![]() 或m≥﹣
或m≥﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,正方形
 的边长为
的边长为 ,动点
,动点 从点
从点 出发,在正方形的边上沿
出发,在正方形的边上沿 运动,设运动的时间为
运动,设运动的时间为 ,点
,点 移动的路程为
移动的路程为 ,
, 与
与 的函数图象如图②,请回答下列问题:
的函数图象如图②,请回答下列问题:
(1)点
 在
在 上运动的时间为
上运动的时间为  ,在
,在 上运动的速度为
上运动的速度为 
(2)设
 的面积为
的面积为 ,求当点
,求当点 在
在 上运动时,
上运动时, 与
与 之间的函数解析式;
之间的函数解析式;(3)①下列图表示
 的面积
的面积 与时间
与时间 之间的函数图象是 .
之间的函数图象是 .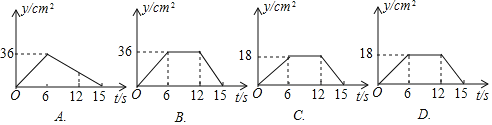
②当

 时,
时, 的面积为
的面积为
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次中学生田径运动会上,参加男子跳高的20名运动员成绩如下所示:
成绩(单位:米)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
4
5
2
1
1
则下列叙述正确的是( )
A. 这些运动员成绩的中位数是1.70
B. 这些运动员成绩的众数是5
C. 这些运动员的平均成绩是1.71875
D. 这些运动员成绩的中位数是1.726
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图像如图所示,则超过500元的部分可以享受的优惠是( )

A. 打六折B. 打七折C. 打八折D. 打九折
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
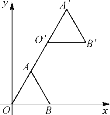
A. (4,2
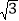 ) B. (3,3) C. (4,3) D. (3,2)
) B. (3,3) C. (4,3) D. (3,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】命题:如果两条平行线被第三条直线所截,那么一组内错角的平分线互相平行,如图为符合该命题的示意图.
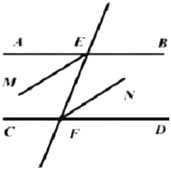
(1)请你根据图形把该命题用几何符号语言补充完整,己知:直线
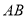 、
、 被第三条直线
被第三条直线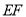 所截,且
所截,且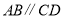 ,
,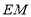 平分
平分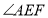 ,
, 平分______,则______
平分______,则______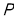 ______
______(2)判断该命题的真假,若是假命题,请举例说明:若是真命题,请证明.
相关试题

