【题目】如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
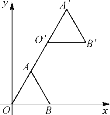
A. (4,2![]() ) B. (3,3) C. (4,3) D. (3,2)
) B. (3,3) C. (4,3) D. (3,2)
参考答案:
【答案】A
【解析】
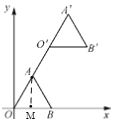
作AM⊥x轴,根据等边三角形的性质得出OA=OB=2,∠AOB=60°,利用含30°角的直角三角形的性质求出OM=![]() OA=1,即可求出AM的长,进而可得A点坐标,即可得出直线OA的解析式,把x=3代入可得A′点的坐标,由一对对应点A与A′的移动规律即可求出点B′的坐标.
OA=1,即可求出AM的长,进而可得A点坐标,即可得出直线OA的解析式,把x=3代入可得A′点的坐标,由一对对应点A与A′的移动规律即可求出点B′的坐标.
如图,作AM⊥x轴于点M,
∵等边△OAB的顶点B坐标为(2,0),
∴OA=OB=2,∠AOB=60°,
∴OM=![]() OA=1,AM=
OA=1,AM=![]() OM=
OM=![]() ,
,
∴A(1,![]() ),
),
∴直线OA的解析式为:y=![]() x,
x,
∴当x=3时,y=3![]() ,
,
∴A′(3,3![]() ),
),
∴将A点向右平移2个单位,再向上平移2![]() 个单位后得到A′点,
个单位后得到A′点,
∴将B(2,0)向右平移2个单位,再向上平移2![]() 个单位后可得到B′点,
个单位后可得到B′点,
∴点B′的坐标为(4,2![]() ),
),
故选A
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次中学生田径运动会上,参加男子跳高的20名运动员成绩如下所示:
成绩(单位:米)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
4
5
2
1
1
则下列叙述正确的是( )
A. 这些运动员成绩的中位数是1.70
B. 这些运动员成绩的众数是5
C. 这些运动员的平均成绩是1.71875
D. 这些运动员成绩的中位数是1.726
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图像如图所示,则超过500元的部分可以享受的优惠是( )

A. 打六折B. 打七折C. 打八折D. 打九折
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题:如果两条平行线被第三条直线所截,那么一组内错角的平分线互相平行,如图为符合该命题的示意图.
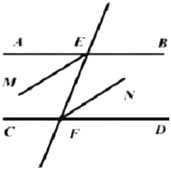
(1)请你根据图形把该命题用几何符号语言补充完整,己知:直线
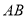 、
、 被第三条直线
被第三条直线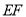 所截,且
所截,且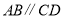 ,
,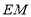 平分
平分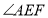 ,
, 平分______,则______
平分______,则______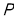 ______
______(2)判断该命题的真假,若是假命题,请举例说明:若是真命题,请证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.
已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:(A组:x<155;B组:155≤x<160;C组:160≤x<165;D组165≤x<170;E组:x≥170)
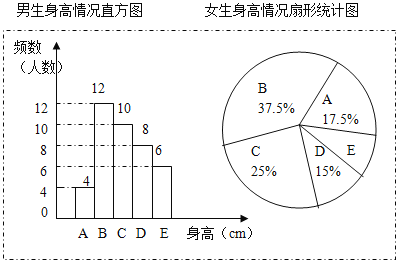
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组.
(2)样本中,女生的身高在E组的人数有 人.
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(1)求证:AEFD=AFEC;
(2)求证:FC=FB;
(3)若FB=FE=2,求⊙O的半径r的长.

相关试题

