【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)

参考答案:
【答案】21m
【解析】试题分析:过点D作DH⊥BC于点M,得出四边形DECH是矩形,所以DH=EC,DE=HC,设BC的长度为xm,则BH=(x-5)m,由∠BDH=30°可以求出∠DBH=60°,进而表示出DH=![]() (x-5),然后表示出AC=
(x-5),然后表示出AC=![]() (x-5)-10,最后由BC= tan50°·AC列出方程,解出x即可.
(x-5)-10,最后由BC= tan50°·AC列出方程,解出x即可.
试题解析:
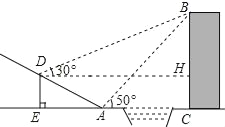
过点D作DH⊥BC于点M,
则四边形DHCE是矩形,DH=EC,DE=HC,
设BC的高度为xm,则BH=(x-5)m,
∵∠BDH=30°,
∴∠DBH=60°,
∴DH=BH·tan60°=![]() (x-5),
(x-5),
∴AC=EC-EA=![]() (x-5)-10,
(x-5)-10,
∵∠BAC=50°,
∴BC= tan50°·AC,
∴x=tan50°·[![]() (x-5)],
(x-5)],
解得:x≈21,
答:建筑物BC的高约为21m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩摸球游戏:一个不透明的袋子中装有相同大小的3个球,球上分别标有数字1,2,3.首先,甲从中随机摸出一个球,然后,乙从剩下的球中随机摸出一个球,比较球上的数字,较大的获胜.
(1)求甲摸到标有数字3的球的概率;
(2)这个游戏公平吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2k+3)x+k2=0有两个不相等的实数根x1,x2.若
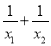 =﹣1,则k的值为_____.
=﹣1,则k的值为_____. -
科目: 来源: 题型:
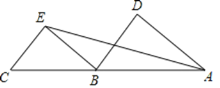
查看答案和解析>>【题目】已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件
 设每件童装降价x元
设每件童装降价x元 时,平均每天可盈利y元.
时,平均每天可盈利y元. 写出y与x的函数关系式;
写出y与x的函数关系式; 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元? 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

相关试题

