【题目】已知关于x的一元二次方程x2+(2k+3)x+k2=0有两个不相等的实数根x1,x2.若![]() =﹣1,则k的值为_____.
=﹣1,则k的值为_____.
参考答案:
【答案】3.
【解析】
利用根与系数的关系结合![]() =﹣1可得出关于k的方程,解之可得出k的值,由方程的系数结合根的判别式△>0可得出关于k的不等式,解之即可得出k的取值范围,进而可确定k的值,此题得解.
=﹣1可得出关于k的方程,解之可得出k的值,由方程的系数结合根的判别式△>0可得出关于k的不等式,解之即可得出k的取值范围,进而可确定k的值,此题得解.
∵关于x的一元二次方程x2+(2k+3)x+k2=0的两根为x1,x2,
∴x1+x2=﹣(2k+3),x1x2=k2,
∴![]() =
=![]() =﹣
=﹣![]() =﹣1,
=﹣1,
解得:k1=﹣1,k2=3.
∵关于x的一元二次方程x2+(2k+3)x+k2=0有两个不相等的实数根,
∴△=(2k+3)2﹣4k2>0,
解得:k>﹣![]() ,
,
∴k1=﹣1舍去.
∴k=3.
故答案为:3.
-
科目: 来源: 题型:
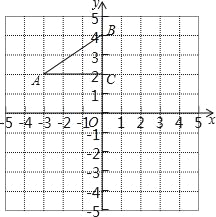
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在图中标明旋转中心P的位置并写出其坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩摸球游戏:一个不透明的袋子中装有相同大小的3个球,球上分别标有数字1,2,3.首先,甲从中随机摸出一个球,然后,乙从剩下的球中随机摸出一个球,比较球上的数字,较大的获胜.
(1)求甲摸到标有数字3的球的概率;
(2)这个游戏公平吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)

-
科目: 来源: 题型:
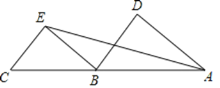
查看答案和解析>>【题目】已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件
 设每件童装降价x元
设每件童装降价x元 时,平均每天可盈利y元.
时,平均每天可盈利y元. 写出y与x的函数关系式;
写出y与x的函数关系式; 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元? 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由.
相关试题

