【题目】如图,在正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.请在给出的5×5的正方形网格中,以格点为顶点,画出两个三角形,一个三角形的长分别是 ![]() 、2、
、2、 ![]() ,另一个三角形的三边长分别是
,另一个三角形的三边长分别是 ![]() 、2
、2 ![]() 、5
、5 ![]() .(画出的两个三角形除顶点和边可以重合外,其余部分不能重合)
.(画出的两个三角形除顶点和边可以重合外,其余部分不能重合) 
参考答案:
【答案】解:△ABC中,AC= ![]() ,AB=2,BC=
,AB=2,BC= ![]() , △DEF中,DF=
, △DEF中,DF= ![]() ,EF=2
,EF=2 ![]() ,DE=5
,DE=5 ![]() .
.
则△ABC和△DEF即为所求.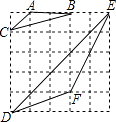
【解析】根据勾股定理在正方形网格中画出三角形的三边长,得到所求的三角形.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF= .
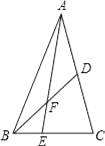
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式3x|m|y2+(m+2)x2y﹣1是四次三项式,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙两个圆柱形容器(容器足够高),底面半径之比为1∶2,用一个管子在甲、乙两个容器的15厘米高度处连通(即管子底端离容器底15厘米).已知只有乙容器中有水,水位高2厘米,如图所示.现同时向甲、乙两个容器注水,平均每分钟注入乙容器的水量是注入甲容器水量的k倍.开始注水1分钟,甲容器的水位上升a厘米,且比乙容器的水位低1厘米.其中a,k均为正整数,当甲、乙两个容器的水位都到达连通管子的位置时,停止注水.甲容器的水位有2次比乙容器的水位高1厘米,设注水时间为t分钟.

(1)求k的值(用含a的代数式表示).
(2)当甲容器的水位第一次比乙容器的水位高1厘米时,求t的值.
(3)当甲容器的水位第二次比乙容器的水位高1厘米时,求a,k,t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF= .
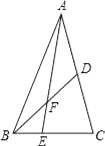
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在ABCD中,E是AD边的中点,连接BE.
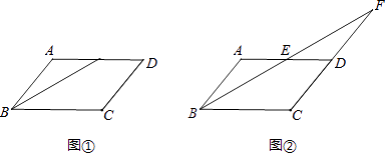
(1)如图①,若BC=2,则AE的长=;
(2)如图②,延长BE交CD的延长线于点F,求证:FD=AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三条边距离相等的点是( )
A. 三条高线的交点 B. 三条中线的交点
C. 三个内角平分线的交点 D. 三边垂直平分线的交点
相关试题

