【题目】如图,在矩形![]() 中,点
中,点![]() 在对角线
在对角线![]() 上,以
上,以![]() 的长为半径的圆
的长为半径的圆![]() 与
与![]() 分别交于点
分别交于点![]() ,且
,且![]() .
.
(1)求证:![]() 是圆
是圆![]() 所在圆的切线;
所在圆的切线;
(2)若![]() ,
,![]() ,求⊙O的半径.
,求⊙O的半径.

参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】分析:
(1)如下图,连接OE,由已知条件易证∠DAC=∠ACB=∠DCE,∠AEO=∠DAC,由此可得∠AEO=∠DCE,结合∠DCE+∠AEC=90°,可得∠AEO+∠DEC=90°从而可得∠CEO=180°-90°=90°,由此可得OE⊥CE,从而可得OE是⊙O的切线;
(2)由tan∠BAC=![]() ,BC=2可得AB=
,BC=2可得AB=![]() 由此可得CD=
由此可得CD=![]() ,AC=
,AC=![]() ,由∠DCE=∠ACB可得tan∠DCE=tan∠ACB=
,由∠DCE=∠ACB可得tan∠DCE=tan∠ACB=![]() ,则DE=DCtan∠DCE=1,这样在Rt△DCE中可得CE=
,则DE=DCtan∠DCE=1,这样在Rt△DCE中可得CE=![]() ,设⊙O的半径为r,在Rt△CEO中由勾股定理建立方程,解方程即可求得r的值.
,设⊙O的半径为r,在Rt△CEO中由勾股定理建立方程,解方程即可求得r的值.
详解:
(1)∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE,
连接OE,则∠DAC=∠AEO=∠DCE,
∵∠DCE+∠DEC=90°,
∴∠AEO+∠DEC=90°,
∴∠OEC=90°,即OE⊥CE,
又OE是⊙O的半径,
∴直线CE与⊙O相切 ;
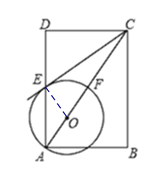
(2)∵tan∠BAC=![]() ,BC=2,
,BC=2,
∴AB =![]() ,
,
∴AC=![]() ,
,
∵∠DCE=∠ACB,
∴tan∠DCE=tan∠ACB=![]() ,
,
∴DE=DCtan∠DCE=1,
在Rt△CDE中,CE=![]() ,
,
设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,
即![]() ,
,
解得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C三点在同一条直线上,若AB=10cm,BC=4cm,D是线段AC的中点,则AD的长为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)10﹣(﹣5)+(﹣9)+6;
(2)﹣14﹣5×[2﹣(﹣3)2];
(3)﹣2+(﹣
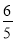 )×(﹣
)×(﹣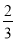 )+(﹣
)+(﹣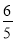 )×
)×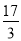
(4)|π-4|+|3-π|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知把直线y=kx+b(k≠0)沿着y轴向上平移3个单位后,得到直线y=﹣2x+5.
(1)求直线y=kx+b(k≠0)的解析式;
(2)求直线y=kx+b(k≠0)与坐标轴围成的三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CE∥BF,CE=BF.则添加下列条件还不能使△EAC≌△FDB.( )

A. AB=CDB. AE∥DFC. ∠E=∠FD. AE=DF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )

A. 4处B. 3处C. 2处D. 1处
相关试题

