【题目】为鼓励居民节约用电,电力公司规定如下电费计算方法:每月用电不超过100度,按每度0.6元计费;每月用电超过100度,超过部分按每度1元计费.
(1)若某用户某年1月交电费88元,那么该用户1月份用电多少度?
(2)若某用户某年2月份平均每度电费0.75元,那么该用户2月份用电多少度?应交电费多少元?
参考答案:
【答案】(1)128;(2)160度,120元.
【解析】
根据题意可知,电费计算方法为:每月用电不超过100度,按每度0.6元计费;每月用电超过100度,超过部分按每度1元计费.
(1)如果用电100度,则需交电费100×0.6=60元,某用户交电费88元,![]() 则该用户用电超过100度,设该用户1月份用电
则该用户用电超过100度,设该用户1月份用电![]() 度,根据题意列出方程求解即可.
度,根据题意列出方程求解即可.
(2)由于此用户平均每度电费0.75元,所以其用电一定超过100度,所以可设此用户2月份共用电![]() 度,则其按每度0.6元费的为100度,按每度1元交费的为
度,则其按每度0.6元费的为100度,按每度1元交费的为![]() 度,由此可得等量关系式:
度,由此可得等量关系式:![]() 解此方程即得用电多少度,进而求出应交电费多少元.
解此方程即得用电多少度,进而求出应交电费多少元.
(1)如果用电100度,则需交电费100×0.6=60元,某用户交电费88元,![]() 则该用户用电超过100度,
则该用户用电超过100度,
设该用户1月份用电![]() 度,
度,
![]()
解得:![]()
答:设该用户1月份用电128度.
(2)设此用户2月份共用电![]() 度,
度,
![]()
解得:![]()
当![]() 时,
时,![]() 元.
元.
答:该用户2月份用电160度,应交电费,120元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第块.

-
科目: 来源: 题型:
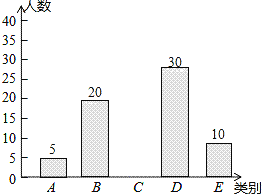
查看答案和解析>>【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别
时间t(小时)
人数
A
t≤0.5
5
B
0.5<t≤1
20
C
1<t≤1.5
a
D
1.5<t≤2
30
E
t>2
10
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)若把每天进行体育锻炼的时间在1小时以上定为锻炼达标,则被抽查学生的达标率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角).

(1)若∠P2P3B=45°,CP1=;
(2)若 <BP3<
<BP3<  ,则P1C长的取值范围是 .
,则P1C长的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L:y=-
 x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.

-
科目: 来源: 题型:
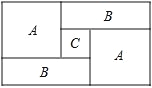
查看答案和解析>>【题目】如图,一个长方形运动场被分割成 A、B、A、B、C 共 5 个区域,A 区域是边长为 a 米的正方形,C 区是边长为 c 米的正方形
(1)列式表示一个 B 区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)当a=4,c=2时,求运动场地的周长和面积.
相关试题

