【题目】(操作发现)如图1,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,先将三角板的
,先将三角板的![]() 角与
角与![]() 重合,再将三角板绕点
重合,再将三角板绕点![]() 按顺时针方向旋转(旋转角大于
按顺时针方向旋转(旋转角大于![]() 且小于
且小于![]() ),旋转后三角板的一直角边与
),旋转后三角板的一直角边与![]() 交于点
交于点![]() .在三角板另一直角边上取一点
.在三角板另一直角边上取一点![]() ,使
,使![]() ,线段
,线段![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .
.

(1)请求出![]() 的度数?
的度数?
(2)![]() 与
与![]() 相等吗?请说明理由;
相等吗?请说明理由;
(类比探究)如图2,![]() 为等边三角形,先将三角板中的
为等边三角形,先将三角板中的![]() 角与
角与![]() 重合,再将三角板绕点
重合,再将三角板绕点![]() 按顺时针方向旋转(旋转角大于
按顺时针方向旋转(旋转角大于![]() 且小于
且小于![]() ).旋转后三角板的一直角边与
).旋转后三角板的一直角边与![]() 交于点
交于点![]() .在三角板斜边上取一点
.在三角板斜边上取一点![]() ,使
,使![]() ,线段
,线段![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .
.
(3)直接写出![]() _________度;
_________度;
(4)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
参考答案:
【答案】(1)![]() ;(2)相等,理由详见解析;(3)
;(2)相等,理由详见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据全等三角形的判定得出![]() ,再由全等三角形的性质得到
,再由全等三角形的性质得到![]() 、
、![]() ,然后根据等腰三角形的判定和性质即可得解;
,然后根据等腰三角形的判定和性质即可得解;
(2)根据全等三角形的判定得出![]() ,再由全等三角形的性质得证结论;
,再由全等三角形的性质得证结论;
(3)根据全等三角形的判定得出![]() ,再由全等三角形的性质得到
,再由全等三角形的性质得到![]() 、
、![]() ,然后根据等边三角形的判定和性质即可得解;
,然后根据等边三角形的判定和性质即可得解;
(4)过点![]() 作
作![]() 于点
于点![]() 交
交![]() 延长线于点
延长线于点![]() ,构造出
,构造出![]() ,利用含
,利用含![]() 角的直角三角形的性质求得
角的直角三角形的性质求得![]() ,再根据勾股定理求得
,再根据勾股定理求得![]() ,最后由勾股定理即可求得答案.
,最后由勾股定理即可求得答案.
解:(1)∵![]() 为等腰直角三角形,且
为等腰直角三角形,且![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴![]() ,
,![]()
∴![]() ;
;
(2)相等,理由如下:
∵![]() ,
,![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴ ![]() .
.
(3)∵![]() 为等边三角形
为等边三角形
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴![]()
∴![]() ;
;
(4)过点![]() 作
作![]() 于点
于点![]() 交
交![]() 延长线于点
延长线于点![]() ,如图:
,如图:

∵由(3)可知,![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]() ,
,![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1)(1,1),(1,2),(2,2)……根据这个规律,第2019个点的坐标为________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
(1) △ABC三个顶点的坐标分别为A( , ),B( , ),C( , );
(2) 是否存在点P,使得
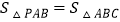 ?若存在,求出满足条件的所有点P的坐标.
?若存在,求出满足条件的所有点P的坐标. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C =∠OAB =108°,F点在线段CB上,OB平分∠AOF,OE平分∠COF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平移AB,那么∠OBC与∠OFC的度数比是否随着AB位置变化而变化?若变化,找出变化规律;若不变,求出这个比值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是( )
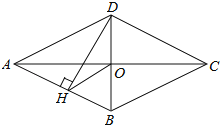
A.20°B.25°C.30°D.40°
-
科目: 来源: 题型:
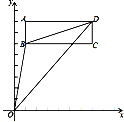
查看答案和解析>>【题目】如图,在长方形ABCD中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出点D的坐标;
(2)连接线段OB,OD,BD,请求出△OBD的面积;
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,设运动的时间为t秒,是否存在某一时刻,使△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
相关试题

