搜索
【题目】在长方形ABCD内，将两张边长分别为a和b(a>b)的正方形纸片按图1，图2两种方式放置(图1，图2中两张正方形纸片均有部分重叠)，设图1中未被这两张正方形纸片覆盖的面积为S1，图2中未被这两张正方形纸片覆盖的面积为S2，当S2-S1=b时，AD-AB的值为（ ）
A.1B.2C.2a-2bD.b
参考答案：
【答案】A
【解析】
根据图1、图2的放置方式，分别用含AB、AD、a、b的代数式表示出S1、S2，进而可得S1-S2，根据S2-S1=b即可得答案.
∵矩形ABCD，
∴AD=BC，AB=CD
由图1和图2可知
S1=a（AB-a）+（AB-b）（AD-a）=AB·AD-a2-AD·b+ab；
S2=AB（AD-a）+（AB-a）（a-b）=AB·AD-a2-AB·b+ab；
∴S2-S1=（AB·AD-a2-AB·b+ab）-（AB·AD-a2-AB·b+ab）
=（AD-AB）·b；
∵S2-S1=b，
∴（AD-AB）·b=b
∴b（AD-AB-1）=0，
∵b≠0
∴AD-AB-1=0
解得：AD-AB=1
故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线
与x轴交于点A、B（点A位于点B左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．（1）求点A、B、C的坐标；
（2）设动点N（-2，n），求使MN+BN的值最小时n的值；
（3）P是抛物线上位于x轴上方的一点，请探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某“欣欣”奶茶店开业大酬宾推出
四款饮料．
千克
饮料的原料是
千克苹果，
千克梨，千克西瓜；1千克
饮料的原料是千克苹果，千克梨，千克西瓜；千克
饮料的原料是千克苹果，
千克梨， 
千克西瓜；千克
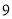饮料的原料是千克苹果，千克梨，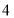
千克西瓜；如果每千克苹果的成本价为元，每千克梨的成本价为
元，每千克西瓜的成本价为
元．开业当天全部售罄，销售后，共计苹果的总成本为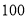
元，并且梨的总成本为
元，那么西瓜的总成本为_____元 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则BC：AB的值为 ▲ 。
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了促进学生多样化发展，某校组织开展了社团活动，分别设置了体育类、艺术类、文学类及其它类社团（要求人人参与社团，每人只能选择一项）．为了解学生喜爱哪种社团活动，学校做了一次抽样调查．根据收集到的数据，绘制成如下两幅不完整的统计图，请根据图中提供的信息，完成下列问题：
（1）此次共调查了多少人？
（2）求文学社团在扇形统计图中所占圆心角的度数；
（3）请将条形统计图补充完整；
（4）若该校有1500名学生，请估计喜欢体育类社团的学生有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图的方格地面上，标有编号A、B、C的3个小方格地面是空地，另外6个小方格地面是草坪，除此以外小方格地面完全相同．
（1）一只自由飞行的鸟，将随意地落在图中的方格地面上，问小鸟落在草坪上的概率是多少？
（2）现从3个小方格空地中任意选取2个种植草坪，则刚好选取A和B的2个小方格空地种植草坪的概率是多少（用树形图或列表法求解）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某县特色早餐种类繁多，色香味美，著名的种类有“干挑面”、“锅贴”、“青团子” “粢米饭”等.一数学兴趣小组在全校范围内随机抽取了一些同学进行“我最喜爱的特色早餐”调查活动，每位同学选择一种自己最喜欢的早餐种类，将调查结果绘制成如下两幅不完整的统计图．请根据图中的信息，解答下列问题：
（1）请将条形统计图补充完整.
（2）在扇形统计图中，表示“粢米饭”对应的扇形的圆心角是多少度?
（3）该校共有1200名学生，请你估计该校学生中最喜爱“青团子”的学生有多少人?
相关试题
