【题目】如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= ![]() AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是
AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ![]() ,则
,则 ![]() 的值是 .
的值是 . 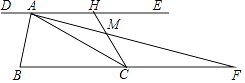
参考答案:
【答案】8﹣ ![]()
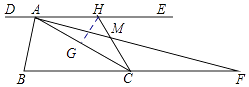
【解析】解:过点H作HG⊥AC于点G, ∵AF平分∠CAE,DE∥BF,
∴∠HAF=∠AFC=∠CAF,
∴AC=CF=2,
∵AM= ![]() AF,
AF,
∴ ![]() =
= ![]() ,
,
∵DE∥CF,
∴△AHM∽△FCM,
∴ ![]() =
= ![]() ,
,
∴AH=1,
设△AHM中,AH边上的高为m,
△FCM中CF边上的高为n,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵△AMH的面积为: ![]() ,
,
∴ ![]() =
= ![]() AHm
AHm
∴m= ![]() ,
,
∴n= ![]() ,
,
设△AHC的面积为S,
∴ ![]() =
= ![]() =3,
=3,
∴S=3S△AHM= ![]() ,
,
∴ ![]() ACHG=
ACHG= ![]() ,
,
∴HG= ![]() ,
,
∴由勾股定理可知:AG= ![]() ,
,
∴CG=AC﹣AG=2﹣ ![]()
∴ ![]() =
= ![]() =8﹣
=8﹣ ![]()
所以答案是:8﹣ ![]()
【考点精析】本题主要考查了相似三角形的判定与性质和解直角三角形的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2
 ,∠AEO=120°,则FC的长度为( )
,∠AEO=120°,则FC的长度为( ) 
A.1
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则
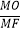 的值为( )
的值为( )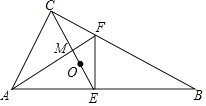
A.
B.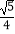
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+
 的最小值为 .
的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算: +cos245°﹣(﹣2)﹣1﹣|﹣
+cos245°﹣(﹣2)﹣1﹣|﹣  |
|
(2)先化简,再求值:( ﹣
﹣  )÷
)÷  ,其中x=2
,其中x=2  ,y=
,y=  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182
195
201
179
208
204
186
192
210
204
175
193
200
203
188
197
212
207
185
206
188
186
198
202
221
199
219
208
187
224
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:谷粒颗数
175≤x<185
185≤x<195
195≤x<205
205≤x<215
215≤x<225
频数
8
10
3
对应扇形图中区域
D
E
C

如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株? -
科目: 来源: 题型:
查看答案和解析>>【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
相关试题

