【题目】如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则 ![]() 的值为( )
的值为( )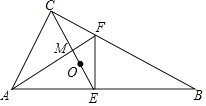
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:∵点O是△ABC的重心,
∴OC= ![]() CE,
CE,
∵△ABC是直角三角形,
∴CE=BE=AE,
∵∠B=30°,
∴∠FAE=∠B=30°,∠BAC=60°,
∴∠FAE=∠CAF=30°,△ACE是等边三角形,
∴CM= ![]() CE,
CE,
∴OM= ![]() CE﹣
CE﹣ ![]() CE=
CE= ![]() CE,即OM=
CE,即OM= ![]() AE,
AE,
∵BE=AE,
∴EF= ![]() AE,
AE,
∵EF⊥AB,
∴∠AFE=60°,
∴∠FEM=30°,
∴MF= ![]() EF,
EF,
∴MF= ![]() AE,
AE,
∴ ![]() =
= ![]() =
= ![]() .
.
故选:D.
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0).
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.
①当点P'落在该抛物线上时,求m的值;
②当点P'落在第二象限内,P'A2取得最小值时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )

A.10m
B.12m
C.12.4m
D.12.32m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2
 ,∠AEO=120°,则FC的长度为( )
,∠AEO=120°,则FC的长度为( ) 
A.1
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+
 的最小值为 .
的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=
 AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是
AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是  ,则
,则 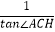 的值是 .
的值是 . 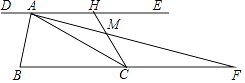
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算: +cos245°﹣(﹣2)﹣1﹣|﹣
+cos245°﹣(﹣2)﹣1﹣|﹣  |
|
(2)先化简,再求值:( ﹣
﹣  )÷
)÷  ,其中x=2
,其中x=2  ,y=
,y=  .
.
相关试题

