【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊的四边形中是勾股四边形的两种图形的名称 、 ;
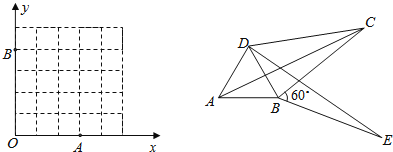
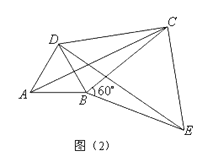
(2)如图1,已知格点(小正方形的顶点)O0,0、A3,0、B0,4,点C 为图中所给方格中的另一个格点,四边形OACB 是以OA 、OB 为勾股边且对角线相等的勾股四边形,求点C 的坐标;
(3)如图2,将ABC( BC AB )绕顶点 B 按顺时针方向旋转60,得到DBE ,连接 AD 、DC ,四边形 ABCD 是勾股四边形,其中DC 、BC 为勾股边,求DCB 的度数.
参考答案:
【答案】(1)矩形,正方形(答案不唯一);(2)C(3,4),(4,3);(3)∠DCB=30°.
【解析】
(1)根据矩形与正方形的性质可得答案;
(2)利用勾股定理可得AB=5,然后在格点中找满足OC=5的点即可;
(3)连接CE,根据旋转的性质可得△ABC≌△DBE,则BC=BE,因为∠CBE=60°,所以△BCE是等边三角形,则BC=CE,∠BCE=60°,根据勾股四边形的定义与勾股定理的逆定理可得∠DCE=90°,则可得∠DCB的度数.
解:(1)矩形;正方形(答案不唯一);
(2)![]() ,
,
则C点坐标如图为:(3,4),(4,3);
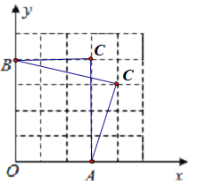
(3)连接CE,
由旋转的性质得:△ABC≌△DBE,则BC=BE,AC=BD,
∵∠CBE=60°,
∴△BCE是等边三角形,
∴BC=CE,∠BCE=60°,
∵四边形ABCD为勾股四边形,其中DC、BC为勾股边,
∴![]() ,
,
∴![]() ,
,
∴∠DCE=90°,
∴∠BCD=∠DCE﹣∠BCE=90°﹣60°=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在ABC 中, BAC 90, AB AC ,点 D 为直线 BC 上的一动点(点 D 不与点 B 、C 重合). 以 AD 为边作正方形 ADEF ,连接CF .
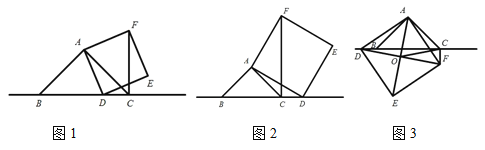
(1)如图 1,当点 D 在线段 BC 上时,求证: BD CF ;
(2)如图 2,当点 D 在线段 BC 的延长线上时,其他条件不变,请直接写出CF 、 BC 、CD 三条线段之间的数量关系;
(3)如图 3,当点 D 在线段 BC 的反向延长线上时,且点 A 、 F 分别在直线 BC 的两侧,其他条件不变, 若正方形 ADEF 的边长为 2 ,对角线 AE 、 DF 相交于点O ,连接OC ,求OC 的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
2011届
2012届
2013届
2014届
2015届
参与实验的人数
106
110
98
104
112
右手大拇指在上的人数
54
57
49
51
56
频率
0.509
0.518
0.500
0.490
0.500
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )

A. 0.6 B. 0.5 C. 0.45 D. 0.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上A,B两点对应的数分别为-2和8,P为数轴上一点,对应的数为x.
(1)线段PA的长度可表示为_________(用含
 的式子表示);
的式子表示);(2)在数轴上是否存在点P,使得PA-PB=6?若存在,求出x的值;若不存在,请说明理由;
(3)当P为线段AB的中点时,点A,B,P同时开始在数轴上分别以每秒3个单位长度,每秒2个单位长度,每秒1个单位长度沿数轴正方向运动,试问经过几秒,PB=2PA?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC 的边OC 、OA 分别与 x 轴、 y 轴重合, AOC 90,BCO 45, AB // OC , BC 6
 ,点C 的坐标为 9,0.
,点C 的坐标为 9,0.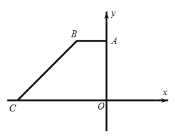

(1)求点 B 的坐标;
(2)若直线 DE 交四边形的对角线 BO 于点 D ,交 y 轴于点 E ,且OE 2 , OD 2BD ,求:
① ODE 的面积;
②点 D 的坐标.
(3)在(2)的条件下,坐标平面内是否存在点 P ,使以O 、E 、P 、D 为顶点的四边形是平行四边形? 若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考前各校初三学生都要进行体育测试,某次中考体育测试设有A、B两处考点,甲、乙、丙三名学生各自随机选择其中的一处进行中考体育测试,请用表格或树状图分析:
(1)求甲、乙、丙三名学生在同一处进行体育测试的概率;
(2)求甲、乙、丙三名学生中至少有两人在B处进行体育测试的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形的上底为
 +2
+2 -10,下底为3
-10,下底为3 -5
-5 -80,高为40.(
-80,高为40.( 取3)
取3)(1)用式子表示图中阴影部分的面积;
(2)当
 =10时,求阴影部分面积的值。
=10时,求阴影部分面积的值。
相关试题

