搜索
【题目】中考前各校初三学生都要进行体育测试，某次中考体育测试设有A、B两处考点，甲、乙、丙三名学生各自随机选择其中的一处进行中考体育测试，请用表格或树状图分析：
（1）求甲、乙、丙三名学生在同一处进行体育测试的概率；
（2）求甲、乙、丙三名学生中至少有两人在B处进行体育测试的概率．
参考答案：
【答案】（1）
（2）
【解析】试题分析：（1）画树状图展示所有8种等可能的结果数，再找出甲、乙、丙三名学生在同一处进行体育测试的结果数，然后根据概率公式求解即可；
（2）找出甲、乙、丙三名学生中至少有两人在B处进行体育测试的结果数，然后根据概率公式求解即可．
试题解析：（1）画树状图为：
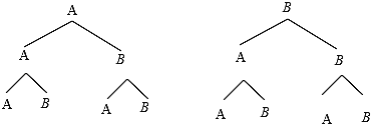
共有8种等可能的结果数，其中甲、乙、丙三名学生在同一处进行体育测试的结果数为2，
所以甲、乙、丙三名学生在同一处进行体育测试的概率P=
；
（2）甲、乙、丙三名学生至少有两人在B处进行体育测试的结果数为4， 所以甲、乙、丙三名学生至少有两人在B处进行体育测试的概率P=
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上A，B两点对应的数分别为-2和8，P为数轴上一点，对应的数为x．
（1）线段PA的长度可表示为_________（用含
的式子表示）；（2）在数轴上是否存在点P，使得PA-PB=6？若存在，求出x的值；若不存在，请说明理由；
（3）当P为线段AB的中点时，点A，B，P同时开始在数轴上分别以每秒3个单位长度，每秒2个单位长度，每秒1个单位长度沿数轴正方向运动，试问经过几秒，PB=2PA？
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊的四边形中是勾股四边形的两种图形的名称 、 ；
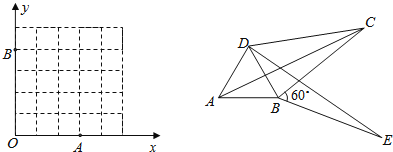
(2)如图1，已知格点（小正方形的顶点）O0,0、A3,0、B0,4，点C 为图中所给方格中的另一个格点，四边形OACB 是以OA 、OB 为勾股边且对角线相等的勾股四边形，求点C 的坐标；
(3)如图2，将ABC（ BC AB ）绕顶点 B 按顺时针方向旋转60，得到DBE ，连接 AD 、DC ，四边形 ABCD 是勾股四边形，其中DC 、BC 为勾股边，求DCB 的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，四边形OABC 的边OC 、OA 分别与 x 轴、 y 轴重合， AOC 90，BCO 45， AB // OC ， BC 6
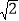，点C 的坐标为 9,0.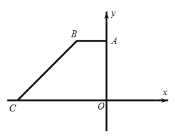
（1）求点 B 的坐标；
（2）若直线 DE 交四边形的对角线 BO 于点 D ，交 y 轴于点 E ，且OE 2 ， OD 2BD ，求：
① ODE 的面积；
②点 D 的坐标.
（3）在（2）的条件下，坐标平面内是否存在点 P ，使以O 、E 、P 、D 为顶点的四边形是平行四边形？ 若存在，请直接写出点 P 的坐标；若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，梯形的上底为
+2
-10，下底为3-5-80，高为40.（
取3）（1）用式子表示图中阴影部分的面积；
（2）当
=10时，求阴影部分面积的值。
-
科目： 来源： 题型：
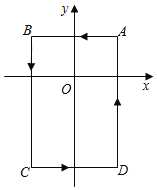
查看答案和解析>>【题目】如图，在平面直角坐标系中，A(1，1)，B(﹣1，1)，C(﹣1，﹣2)，D(1，﹣2)．把一条长为2019个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了决定谁将获得仅有的一张科普报告入场券，甲和乙设计了如下的一个游戏：
口袋中有编号分别为1、2、3的红球三个和编号为4的白球一个，四个球除了颜色或编号不同外，没有任何别的区别，摸球之前将小球搅匀，摸球的人都蒙上眼睛．先甲摸两次，每次摸出一个球；把甲摸出的两个球放回口袋后，乙再摸，乙只摸一个球．如果甲摸出的两个球都是红色，甲得1分，否则，甲得0分；如果乙摸出的球是白色，乙得1分，否则，乙得0分 ；得分高的获得入场券，如果得分相同，游戏重来．
（1）运用列表或画树状图求甲得1分的概率；
（2）这个游戏是否公平？请说明理由．
相关试题
