【题目】已知,在ABC 中, BAC 90, AB AC ,点 D 为直线 BC 上的一动点(点 D 不与点 B 、C 重合). 以 AD 为边作正方形 ADEF ,连接CF .
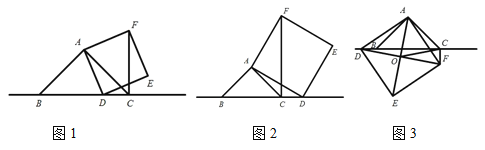
(1)如图 1,当点 D 在线段 BC 上时,求证: BD CF ;
(2)如图 2,当点 D 在线段 BC 的延长线上时,其他条件不变,请直接写出CF 、 BC 、CD 三条线段之间的数量关系;
(3)如图 3,当点 D 在线段 BC 的反向延长线上时,且点 A 、 F 分别在直线 BC 的两侧,其他条件不变, 若正方形 ADEF 的边长为 2 ,对角线 AE 、 DF 相交于点O ,连接OC ,求OC 的长度.
参考答案:
【答案】(1)证明见解析;(2)CF=BC+CD;(3)OC=![]() .
.
【解析】
(1)根据等腰直角三角形与正方形的性质,通过“边角边”证明△BAD≌△CAF,则BD=CF;
(2)同理(1)通过“边角边”证明△BAD≌△CAF,则BD=CF,可得CF=BC+CD;
(3)同上通过“边角边”证明△BAD≌△CAF,得到∠ACF=∠ABD=∠BAC+∠BCA,则∠DCF=90°,在Rt△DCF中OC是斜边上的中线,则OC=![]() DF,然后根据正方形的边长求得其对角线的长即可得到答案.
DF,然后根据正方形的边长求得其对角线的长即可得到答案.
解:(1)∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∵BAC 90,
∴∠BAD+∠CAD=90°,∠CAF+∠CAD=90°,
∴∠BAD=∠CAF,
又∵AB=C,
∴△BAD≌△CAF(SAS),
∴BD=CF;
(2)∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∵BAC 90,
∴∠BAD=∠CAD+90°,∠CAF=∠CAD+90°,
∴∠BAD=∠CAF,
又∵AB=AC,
∴△BAD≌△CAF(SAS),
∴BD=CF=BC+CD;
(3)同理(1)易证△BAD≌△CAF(SAS),
∴∠ABD=∠ACF,
∵∠ABD=∠BAC+∠BCA,∠ACF=∠BCA+∠BCF,
∴∠BCF=∠BCA=90°,
则在Rt△DCF中,
∵DO=FO,
∴OC=![]() DF,
DF,
∵正方形ADEF的边长为2,
∴DF=2![]() ,
,
则OC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
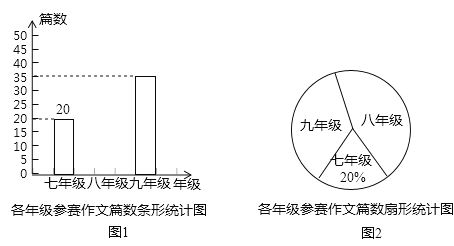
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
-
科目: 来源: 题型:
查看答案和解析>>【题目】
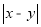 的意义是数轴上表示x、y 的两点之间的距离。例如:
的意义是数轴上表示x、y 的两点之间的距离。例如: 表示4与 —2 的差的绝对值,实际上也可以理解为 4 与—2 两数在数轴上所对应的两点之间的距离;同理
表示4与 —2 的差的绝对值,实际上也可以理解为 4 与—2 两数在数轴上所对应的两点之间的距离;同理 也可以理解为 x 与 3 两数在数轴上所对应的两点之间的距离。试探索:
也可以理解为 x 与 3 两数在数轴上所对应的两点之间的距离。试探索:(1)
 = ;
= ;(2)若
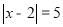 ,则 x= ;
,则 x= ;(3)请你找出符合条件的整数x ,使得

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
2011届
2012届
2013届
2014届
2015届
参与实验的人数
106
110
98
104
112
右手大拇指在上的人数
54
57
49
51
56
频率
0.509
0.518
0.500
0.490
0.500
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )

A. 0.6 B. 0.5 C. 0.45 D. 0.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上A,B两点对应的数分别为-2和8,P为数轴上一点,对应的数为x.
(1)线段PA的长度可表示为_________(用含
 的式子表示);
的式子表示);(2)在数轴上是否存在点P,使得PA-PB=6?若存在,求出x的值;若不存在,请说明理由;
(3)当P为线段AB的中点时,点A,B,P同时开始在数轴上分别以每秒3个单位长度,每秒2个单位长度,每秒1个单位长度沿数轴正方向运动,试问经过几秒,PB=2PA?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊的四边形中是勾股四边形的两种图形的名称 、 ;
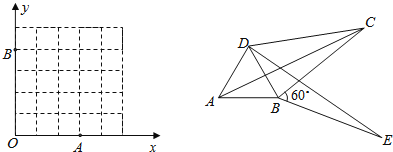
(2)如图1,已知格点(小正方形的顶点)O0,0、A3,0、B0,4,点C 为图中所给方格中的另一个格点,四边形OACB 是以OA 、OB 为勾股边且对角线相等的勾股四边形,求点C 的坐标;
(3)如图2,将ABC( BC AB )绕顶点 B 按顺时针方向旋转60,得到DBE ,连接 AD 、DC ,四边形 ABCD 是勾股四边形,其中DC 、BC 为勾股边,求DCB 的度数.
相关试题

