搜索
【题目】如图，点M、N分别是正五边形ABCDE的边BC、CD上的点，且BM=CN，AM交BN于点P．
（1）求证：△ABM≌△BCN；
（2）求∠APN的度数．
参考答案：
【答案】（1）证明见解析；
（2）∠APN的度数为108°．
【解析】
试题（1）利用正五边形的性质得出AB=BC，∠ABM=∠C，再利用全等三角形的判定得出即可；
（2）利用全等三角形的性质得出∠BAM+∠ABP=∠APN，进而得出∠CBN+∠ABP=∠APN=∠ABC即可得出答案．
试题解析：（1）∵正五边形ABCDE，
∴AB=BC，∠ABM=∠C，
∴在△ABM和△BCN中
，
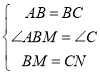∴△ABM≌△BCN（SAS）；
（2）∵△ABM≌△BCN，
∴∠BAM=∠CBN，
∵∠BAM+∠ABP=∠APN，
∴∠CBN+∠ABP=∠APN=∠ABC=
=108°．
即∠APN的度数为108°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）.
(1) 请画出△ABC向左平移5个单位长度后得到的△A
B
C
；(2) 请画出△ABC关于原点对称的△A
B
C
；(3) 在
轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，∠A=∠C=90°，BE，DF分别是∠ABC，∠ADC的平分线．
（1）∠1与∠2有什么关系，为什么？
（2）BE与DF有什么关系？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费，某顾客刚好消费200元．
（1）该顾客至少可得到元购物券，至多可得到元购物券；
（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高2米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有25米的距离（B，F，C在一条直线上）．
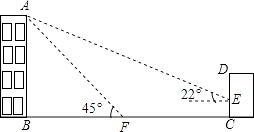
（参考数据：sin22°≈
，cos22°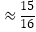 
，tan22 
）
（1）求办公楼AB的高度；
（2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AC=BC，∠ACB=120°，点D在AB边上运动（D不与A、B重合），连结CD．作∠CDE=30°，DE交AC于点E．
（1）当DE∥BC时，△ACD的形状按角分类是直角三角形；
（2）在点D的运动过程中，△ECD的形状可以是等腰三角形吗？若可以，请求出∠AED的度数；若不可以，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E，H分别在AB、AC上，已知BC=40cm，AD=30cm．
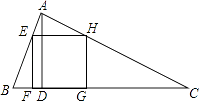
（1）求证：△AEH∽△ABC；
（2）求这个正方形的边长与周长．
相关试题
