【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 . 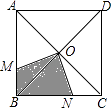
参考答案:
【答案】![]()
【解析】解:∵四边形ABCD为正方形,点O是对角线的交点,
∴∠MBO=∠NCO=45°,OB=OC,∠BOC=90°,
∵∠MON=90°,
∴∠MOB+∠BON=90°,∠BON+∠NOC=90°,
∴∠MOB=∠NOC.
在△MOB和△NOC中,有  ,
,
∴△MOB≌△NOC(ASA).
同理可得:△AOM≌△BON.
∴S阴影=S△BOC= ![]() S正方形ABCD .
S正方形ABCD .
∴蚂蚁停留在阴影区域的概率P= ![]() =
= ![]() .
.
故答案为: ![]() .
.
根据正方形的性质可得出“∠MBO=∠NCO=45°,OB=OC,∠BOC=90”,通过角的计算可得出∠MOB=∠NOC,由此即可证出△MOB≌△NOC,同理可得出△AOM≌△BON,从而可得知S阴影= ![]() S正方形ABCD , 再根据几何概率的计算方法即可得出结论.本题考查了几何概率.正方形的性质以及全等三角形的判断及性质,解题的关键是找出S阴影=S△BOC=
S正方形ABCD , 再根据几何概率的计算方法即可得出结论.本题考查了几何概率.正方形的性质以及全等三角形的判断及性质,解题的关键是找出S阴影=S△BOC= ![]() S正方形ABCD . 本题属于基础题,难度不大,解决该题型题目时,根据正方形的性质和角的计算找出相等的边角关系,再利用全等三角形的判定定理证出三角形全等是关键.
S正方形ABCD . 本题属于基础题,难度不大,解决该题型题目时,根据正方形的性质和角的计算找出相等的边角关系,再利用全等三角形的判定定理证出三角形全等是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,随机地闭合开关S1 , S2 , S3 , S4 , S5中的三个,能够使灯泡L1 , L2同时发光的概率是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】任取不等式组
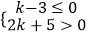 的一个整数解,则能使关于x的方程:2x+k=﹣1的解为非负数的概率为 .
的一个整数解,则能使关于x的方程:2x+k=﹣1的解为非负数的概率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n
1000
1500
2500
4000
8000
15000
20000
30000
成活的棵数m
865
1356
2220
3500
7056
13170
17580
26430
成活的频率

0.865
0.904
0.888
0.875
0.882
0.878
0.879
0.881
估计该种幼树在此条件下移植成活的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知A(a,0),B (0,b)分别为两坐标轴上的点,且a,b满足a2﹣24a+|b﹣12|=﹣144,且3OC=OA.
(1)求A、B、C三点的坐标;
(2)若D(2,0),过点D的直线分别交AB、BC于E、F两点,且DF=DE,设E、F两点的横坐标分别为xE、xP,求xE+xP的值;
(3)如图2,若M(4,8),点P是x轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 .
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 .
(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺序通关的概率.
相关试题

