【题目】已知:在平面直角坐标系中,抛物线![]() (
(![]() )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
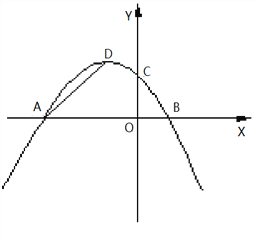
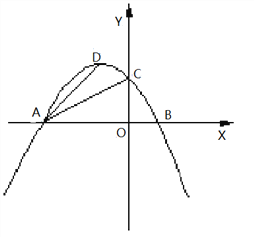
图1 图2
参考答案:
【答案】(1)y=![]() x2x+3.D(-2,4).(2)①当t=3时,W有最大值,W最大值=18.②存在.只存在一点P(0,2)使Rt△ADP与Rt△AOC相似.
x2x+3.D(-2,4).(2)①当t=3时,W有最大值,W最大值=18.②存在.只存在一点P(0,2)使Rt△ADP与Rt△AOC相似.
【解析】试题分析:(1)根据抛物线y=ax2+bx+c(a≠0)对称轴是直线x=![]() ,且已知抛物线
,且已知抛物线![]() (
(![]() )的对称轴为直线x=―2,故
)的对称轴为直线x=―2,故![]() ,可求出 a的值,即可写出抛物线的解析式和顶点坐标;(2)探究一:由抛物线
,可求出 a的值,即可写出抛物线的解析式和顶点坐标;(2)探究一:由抛物线![]() 的解析式可求x、y轴的交点
的解析式可求x、y轴的交点![]() 的坐标,作
的坐标,作![]() 轴于M,则
轴于M,则![]() ,点
,点![]() ,由
,由![]() =
=![]()
![]()
![]() 可得,
可得,![]() ,当
,当![]() 时,W有最大值,
时,W有最大值,![]() ;探究二:分三种情况分析:①当
;探究二:分三种情况分析:①当![]() 时,作
时,作![]() 轴于E,则
轴于E,则![]() ,则
,则![]() ,则
,则![]() ,则
,则![]() ,又因为
,又因为![]() 轴,
轴,![]() 轴,则
轴,则![]() ,则
,则![]() ,
,![]() ,
,![]() ,则此时有
,则此时有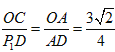 ,又因为
,又因为![]() ,即
,即![]() ,此时
,此时![]() ,则
,则![]() ,所以当
,所以当![]() 时,存在点P1,使
时,存在点P1,使![]() ,此时P1点的坐标为(0,2);②当
,此时P1点的坐标为(0,2);②当![]() 时,则
时,则![]() ,则
,则![]() ,则
,则![]() ,又因为
,又因为![]() ,则
,则![]() ,所以
,所以![]() 与
与![]() 不相似,此时点P2不存在;③当
不相似,此时点P2不存在;③当![]() 时,以AD为直径作,则
时,以AD为直径作,则![]() 的半径
的半径![]() ,圆心O1到y轴的距离
,圆心O1到y轴的距离![]() ,因为
,因为![]() ,所以
,所以![]() 与y轴相离,不存在点P3,使
与y轴相离,不存在点P3,使![]() ,
,
所以综合可得,只存在一点![]() 使
使![]() 与
与![]() 相似。
相似。
试题解析:
(1)∵抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)探究一:当![]() 时,W有最大值,
时,W有最大值,
∵抛物线![]() 交x轴于A、B两点,交y轴于点C,
交x轴于A、B两点,交y轴于点C,
∴![]() ,
,
∴![]() ,
,
当![]() 时,作
时,作![]() 轴于M,如图所示:
轴于M,如图所示:
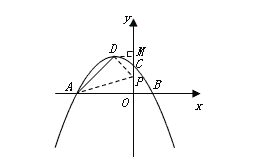
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]()
![]() ,
,![]()
![]()
∴![]()
∴当![]() 时,W有最大值,
时,W有最大值,![]() ,
,
探究二:存在,分三种情况:
①当![]() 时,作
时,作![]() 轴于E,如图所示:
轴于E,如图所示: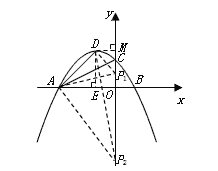
则![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∵![]() 轴,
轴,![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,,
,,
此时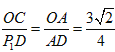 ,又因为
,又因为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,存在点P1,使
时,存在点P1,使![]() ,此时P1点的坐标为(0,2);
,此时P1点的坐标为(0,2);
②当![]() 时,则
时,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 不相似,此时点P2不存在;
不相似,此时点P2不存在;
③当![]() 时,以AD为直径作,则
时,以AD为直径作,则![]() 的半径
的半径![]() ,圆心O1到y轴的距离
,圆心O1到y轴的距离![]() ,∵
,∵![]() ,
,
∴![]() 与y轴相离,不存在点P3,使
与y轴相离,不存在点P3,使![]() ,
,
∴综上所述,只存在一点![]() 使
使![]() 与
与![]() 相似。
相似。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果△ABC与△DEF相似,△ABC的三边之比为3:4:6,△DEF的最长边是10cm,那么△DEF的最短边是 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列说法中错误的是( )
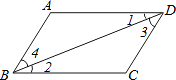
A.∵∠A+∠ADC=180°,∴AB∥CD
B.∵AB∥CD,∴∠ABC+∠C=180°
C.∵∠1=∠2,∴AD∥BC
D.∵AD∥BC,∴∠3=∠4 -
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店因换季将某种服装打折销售,如果每件服装按标价的5折出售将亏本20元,而按标价的8折出售将赚40元.为了保证不亏本,最少要打 折( )
A. 6 B. 6.5 C. 7 D. 7.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】要在一块长52 m,宽48 m的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积.(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)
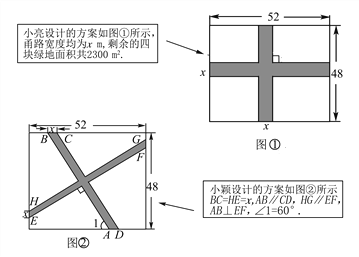
-
科目: 来源: 题型:
查看答案和解析>>【题目】进价为每件20元的玩具,如果以每件30元出售,那么一个月内可以售出180件,根据销售经验:每涨价1元,月销售量减少10件,问涨价多少元时在一个月内的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=AC,E,F分别是BC、AD的中点,连接AE、CF.
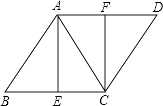
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
相关试题

