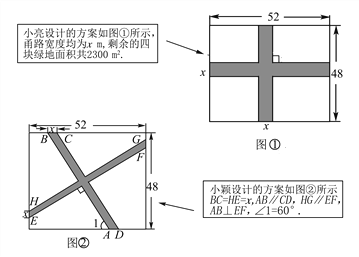
【题目】要在一块长52 m,宽48 m的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积.(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)
参考答案:
【答案】(1) 小亮设计方案中甬路的宽度为2m;(2) 2299m2.
【解析】试题分析:(1)利用平移把互相垂直的小路分别移到左侧和下面,表示出绿地的长和宽,建立绿地面积的一元二次方程求解;(2)由上题知道了甬路的宽,此题绿地面积应该等于矩形面积减去两个平行四边形的面积再加上两个平行四边形重合的小正方形的面积,因为两条甬路为平行四边形,所以求出平行四边形的高是解决问题的关键,过A点作CD边上的高,利用60度的正弦值求出高,即可求出绿地面积.
试题解析:(1)由题意可得,绿地的长为(52-x)m,绿地的宽为(48-x)m,因为绿地面积共2300平方米,所以列方程得:(52-x)(48-x)=2300,去括号得:x2-100x+196=0,解得:x1=2,x2=98(不合题意舍去),所以x=2,即甬路的宽度为2m;(2)过A点作AI⊥CD,HJ⊥EF,垂足分别为I,J,因为AB∥CD,∠1=60°,所以∠ADI=60°,因为BC∥AD,所以四边形ADCB为平行四边形,所以BC=AD,由上题得甬路x=2,所以BC=HE=2=AD,在Rt△ADI中,AI=2sin60°=![]() ,所以绿地面积应该等于矩形面积减去两个平行四边形的面积再加上两个平行四边形重合的小正方形的面积,即为52×48-52×2-48×2+
,所以绿地面积应该等于矩形面积减去两个平行四边形的面积再加上两个平行四边形重合的小正方形的面积,即为52×48-52×2-48×2+![]() =2496-104-96+3=2299(平方米).
=2496-104-96+3=2299(平方米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列说法中错误的是( )
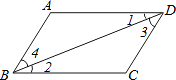
A.∵∠A+∠ADC=180°,∴AB∥CD
B.∵AB∥CD,∴∠ABC+∠C=180°
C.∵∠1=∠2,∴AD∥BC
D.∵AD∥BC,∴∠3=∠4 -
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店因换季将某种服装打折销售,如果每件服装按标价的5折出售将亏本20元,而按标价的8折出售将赚40元.为了保证不亏本,最少要打 折( )
A. 6 B. 6.5 C. 7 D. 7.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,抛物线
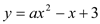 (
(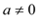 )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
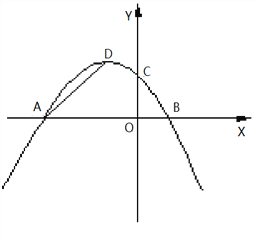
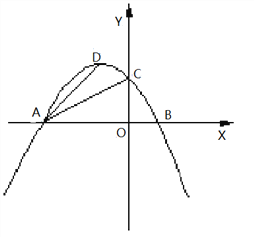
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】进价为每件20元的玩具,如果以每件30元出售,那么一个月内可以售出180件,根据销售经验:每涨价1元,月销售量减少10件,问涨价多少元时在一个月内的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=AC,E,F分别是BC、AD的中点,连接AE、CF.
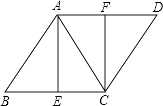
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.
相关试题

