【题目】如果△ABC与△DEF相似,△ABC的三边之比为3:4:6,△DEF的最长边是10cm,那么△DEF的最短边是 cm.
参考答案:
【答案】5
【解析】解:设△DEF的最短边为x,△ABC的三边分别为3a,4a,6a,
∵△ABC与△DEF相似,
∴3a:x=6a:10,
∴x=5,
即△DEF的最短边是5cm.
故答案为5.
设△DEF的最短边为x,由△ABC的三边之比为3:4:6,则可设△ABC的三边分别为3a,4a,6a,由于△ABC与△DEF相似,根据相似三角形的性质得到3a:x=6a:10,即可求出x=5.
-
科目: 来源: 题型:
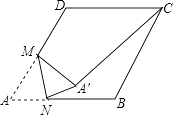
查看答案和解析>>【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出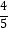 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价) -
科目: 来源: 题型:
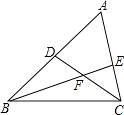
查看答案和解析>>【题目】如图,在△ABC中,∠B,∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A.118°
B.119°
C.120°
D.121° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列说法中错误的是( )
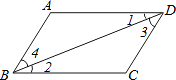
A.∵∠A+∠ADC=180°,∴AB∥CD
B.∵AB∥CD,∴∠ABC+∠C=180°
C.∵∠1=∠2,∴AD∥BC
D.∵AD∥BC,∴∠3=∠4 -
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店因换季将某种服装打折销售,如果每件服装按标价的5折出售将亏本20元,而按标价的8折出售将赚40元.为了保证不亏本,最少要打 折( )
A. 6 B. 6.5 C. 7 D. 7.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,抛物线
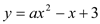 (
(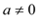 )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
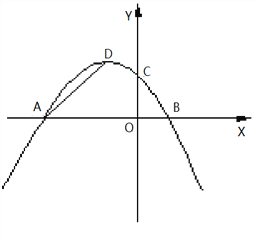
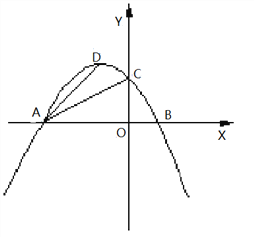
图1 图2
相关试题

