【题目】正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
(1)如图,若tanB=2,则![]() 的值为
的值为
(2)将△ABC绕点D旋转得到△A′B′C′,连接BB′、CC′.若![]() , 则tanB的值为
, 则tanB的值为 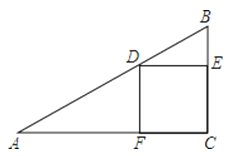
参考答案:
【答案】![]() ;
;![]()
【解析】解:(1)∵四边形CEDF为正方形,
∴ED=EC,∠CED=90°,
在Rt△BDE中,∵tanB=![]() =2,
=2,
∴DE=2BE,
∴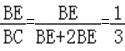
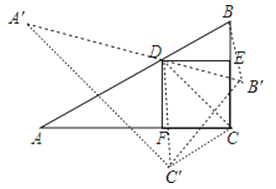
(2)连结DC、DC′,如图,
∵△ABC绕点D旋转得到△A′B′C′,
∴DB=DB′,DC=DC′,∠BDB′=∠CDC′,
即![]()
∴△DBB′∽△DCC′,
∴![]() =
=![]()
设DC=3![]() x,BD=5x,
x,BD=5x,
∵四边形CEDF为正方形,
∴DE=3x,
在Rt△BDE中,BE=![]()
∴tanB=![]()
所以答案是![]() ,
, ![]() .
. 
(1)由正方形的性质得ED=EC,∠CED=90°,再在Rt△BDE中,利用正切的定义得到DE=2BE,则CE=BE,所以![]() =
=![]() ;
;
(2)连结DC、DC′,如图,根据旋转的性质得DB=DB′,DC=DC′,∠BDB′=∠CDC′,则可判断△DBB′∽△DCC′,根据相似三角形的性质得![]() =
=![]() , 则可设DC=3
, 则可设DC=3![]() x,BD=5x,然后利用正方形性质得DE=3x,接着利用勾股定理计算出BE=4x,最后根据正切的定义求解.
x,BD=5x,然后利用正方形性质得DE=3x,接着利用勾股定理计算出BE=4x,最后根据正切的定义求解.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD=
 , 则AB的长为( )
, 则AB的长为( )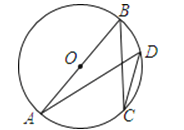
A.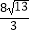
B.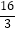
C.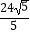
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲; ④乙出发6分钟后追上甲.
其中正确的有_____________(填所有正确的序号).
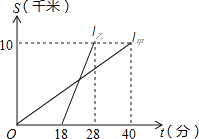
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(x﹣1)(x+1)=x2﹣1,
(x﹣1)(x2+x+1)=x3﹣1,
(x﹣1)(x3+x2+x+1)= ,
…
猜想:(x﹣1)(xn+xn﹣1+…+x2+x+1)= ,
(2)根据以上结果,试写出下面两式的结果
①(x﹣1)(x49+x48+…+x2+x+1)= ,
②(x20﹣1)÷(x﹣1)= ,
(3)利用以上结论求值:1+3+32+33+34+……+32017
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.
(1)求y与x之间的函数关系式?(不要求写自变量的取值范围);
(2)求矩形ABCD的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=﹣
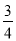 x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.
x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.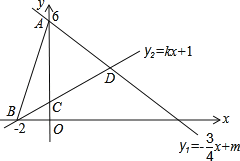
(1)m= ,k= ;
(2)求两直线交点D的坐标;
(3)根据图象直接写出y1<y2时自变量x的取值范围.
相关试题

