【题目】◆探索发现:如图是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图1、图2,弹弓的两边可看成是平行的,即![]() .各活动小组探索
.各活动小组探索![]() 与
与![]() ,
,![]() 之间的数量关系.已知
之间的数量关系.已知![]() ,点
,点![]() 不在直线
不在直线![]() 和直线
和直线![]() 上.在图1中,智慧小组发现:
上.在图1中,智慧小组发现:![]() ;
;

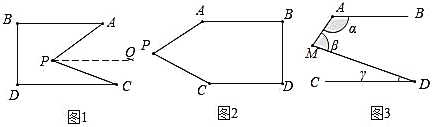
智慧小组是这样思考的:过点![]() 作
作![]() ,……
,……
请你按照智慧小组作的辅助线补全推理过程.
◆类比思考:①在图2中,![]() 与
与![]() ,
,![]() 之间的数量关系为________.
之间的数量关系为________.
②如图3,已知![]() ,则角
,则角![]() 、
、![]() 、
、![]() 之间的数量关系为________.
之间的数量关系为________.
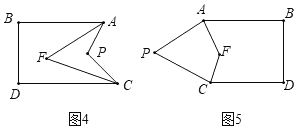
◆解决问题:善思小组提出:如图4,图5.![]() ,
,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() .
.
①在图4中,![]() 与
与![]() 之间的关系为________.
之间的关系为________.
②在图5中,![]() 与
与![]() 之间的关系为________.
之间的关系为________.
参考答案:
【答案】探索发现:见解析;类比思考:①![]() ;②
;②![]() ;解决问题:①
;解决问题:①![]() ;②
;②![]() .
.
【解析】
探索:发现由平行线的性质得出∠APQ=∠A,由PQ∥AB,AB∥CD,推出PQ∥CD,得出∠APQ=∠C,推出∠APQ+∠CPQ=∠A+∠C,即可得出结论;
类比思考①过点P作PQ∥AB,延长BA到M,延长DC到N,由平行线的性质得出∠APQ=∠PAM,由PQ∥AB,AB∥CD,推出PQ∥CD,得出∠APQ=∠PCN,则∠APQ+∠CPQ+∠PAB+∠PCD=360°,即可得出结果;
②过点M作MQ∥AB,由平行线的性质得出α+∠QMA=180°,由MQ∥AB,AB∥CD,推出MQ∥CD,得出∠QMD=γ,即可得出结果;
解决问题①过点P作PQ∥AB,过点F作FM∥AB,由平行线的性质得出∠APQ=∠BAP,∠AFM=∠BAF,由角平分线的性质得出∠BAF=∠PAF,即∠AFM=![]() ∠BAP,由PQ∥AB,FM∥AB,AB∥CD,推出PQ∥CD,FM∥CD,得出∠CPQ=∠DCP,∠CFM=∠DCF,由角平分线的性质得出∠DCF=∠PCF,即∠CFM=
∠BAP,由PQ∥AB,FM∥AB,AB∥CD,推出PQ∥CD,FM∥CD,得出∠CPQ=∠DCP,∠CFM=∠DCF,由角平分线的性质得出∠DCF=∠PCF,即∠CFM=![]() ∠DCP,推出∠APC=∠BAP+∠DCP,∠AFC=
∠DCP,推出∠APC=∠BAP+∠DCP,∠AFC=![]() (∠BAP+∠DCP),即可得出结果;
(∠BAP+∠DCP),即可得出结果;
②过点P作PH∥AB,过点F作FQ∥AB,延长BA到M,延长DC到N,由平行线的性质得出∠APH=∠MAP,∠AFQ=∠BAF,由角平分线的性质得出∠BAF=∠PAF,即2∠AFQ=∠BAP,由PH∥AB,FQ∥AB,AB∥CD,推出PH∥CD,FQ∥CD,得出∠CPH=∠NCP,∠CFQ=∠DCF,由角平分线的性质得出∠DCF=∠PCF,即2∠CFQ=∠DCP,由∠BAP+∠MAP=180°,∠DCP+∠NCP=180°,得出2∠AFQ+∠APH=180°,2∠CFQ+∠CPH=180°,即可得出结果.
探索发现:
∴![]()
∵![]() 、
、![]()
∴![]()
∴![]()
∴![]()
即![]()
类比思考:①∠APC+∠A+∠C=360°;理由如下:
过点P作PQ∥AB,延长BA到M,延长DC到N,如图2所示:
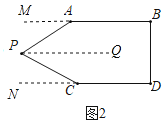
∴∠APQ=∠PAM,
∵PQ∥AB,AB∥CD,
∴PQ∥CD,
∴∠APQ=∠PCN,
∴∠APQ+∠CPQ+∠PAB+∠PCD=180°+180°=360°,
∴∠APC+∠A+∠C=360°,
故答案为:∠APC+∠A+∠C=360°;

②α+β-γ=180°;理由如下:
过点M作MQ∥AB,如图3所示:
∴α+∠QMA=180°,
∵MQ∥AB,AB∥CD,
∴MQ∥CD,
∴∠QMD=γ,
∵∠QMA+∠QMD=β,
∴α+β-γ=180°,
故答案为:α+β-γ=180°;
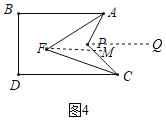
解决问题:①∠AFC=![]() ∠APC;理由如下:
∠APC;理由如下:
过点P作PQ∥AB,过点F作FM∥AB,如图4所示:
∴∠APQ=∠BAP,∠AFM=∠BAF,
∵AF平分∠BAP,
∴∠BAF=∠PAF,
∴∠AFM=![]() ∠BAP,
∠BAP,
∵PQ∥AB,FM∥AB,AB∥CD,
∴PQ∥CD,FM∥CD,
∴∠CPQ=∠DCP,∠CFM=∠DCF,
∵CF平分∠DCP,
∴∠DCF=∠PCF,
∴∠CFM=![]() ∠DCP,
∠DCP,
∴∠APC=∠BAP+∠DCP,∠AFC=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP),
(∠BAP+∠DCP),
∴∠AFC=![]() ∠APC,
∠APC,
故答案为:∠AFC=![]() ∠APC;
∠APC;
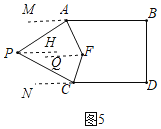
②∠AFC=180°-![]() ∠APC;理由如下:
∠APC;理由如下:
过点P作PH∥AB,过点F作FQ∥AB,延长BA到M,延长DC到N,如图5所示:
∴∠APH=∠MAP,∠AFQ=∠BAF,
∵AF平分∠BAP,
∴∠BAF=∠PAF,
∴2∠AFQ=∠BAP,
∵PH∥AB,FQ∥AB,AB∥CD,
∴PH∥CD,FQ∥CD,
∴∠CPH=∠NCP,∠CFQ=∠DCF,
∵CF平分∠DCP,
∴∠DCF=∠PCF,
∴2∠CFQ=∠DCP,
∵∠BAP+∠MAP=180°,∠DCP+∠NCP=180°,
∴2∠AFQ+∠APH=180°,2∠CFQ+∠CPH=180°,
∴2∠AFQ+∠APH+2∠CFQ+∠CPH=360°,
即2∠AFC+∠APC=360°,
∴∠AFC=180°-![]() ∠APC,
∠APC,
故答案为:∠AFC=180°-![]() ∠APC.
∠APC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表中所列x,y的数值是某二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7 , 根据表中所提供的信息,以下判断正确的是( ).
①a>0;
②9<m<16;
③k≤9;
④b2≤4a(c﹣k).x
…
x1
x2
x3
x4
x5
x6
x7
…
y
…
16
m
9
k
9
m
16
…
A.①②
B.③④
C.①②④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】常用的分解因式的方法有提取公因式法、公式法,但有更多的多项式只用上述方法就无法分解,如x2﹣4y2﹣2x+4y,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为:x2﹣4y2﹣2x+4y=(x+2y)(x﹣2y)﹣2(x﹣2y)=(x﹣2y)(x+2y﹣2),这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.
(1)分解因式:x2+2xy+y2;
(2)分解因式:a2﹣9﹣2ab+b2;
(3)△ABC三边a、b、c满足a2﹣4bc+4ac﹣ab=0,判断△ABC的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮家距离学校8千米,一天早晨小亮骑车上学,途中恰好遇到交警叔叔在十字路口带领小朋友过马路,小亮停下车协助交警叔叔,几分钟后,为了不迟到,他加快了骑车到校的速度.到校后,小亮根据这段经历画出了过程图象如图.该图象描绘了小亮骑行的路程
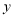 (千米)与他所用的时间
(千米)与他所用的时间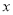 (分钟)之间的关系,请根据图象,解答下列问题:
(分钟)之间的关系,请根据图象,解答下列问题: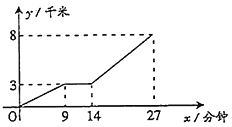
(1)小亮骑车行驶了多少千米时,协助交警叔叔?协助交警叔叔用了几分钟?
(2)小亮从家出发到学校共用了多少时间?
(3)如果没有协助交警叔叔,仍保持出发时的速度行驶,那么他比实际情况早到或晚到学校多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
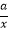 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 
(1)求函数y=kx+b和y=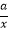 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市实行中考改革,需要根据该市中学体能的实际情况重新制定中考体育标准.为此,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试.测试的情况绘制成表格如下:
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少?
次数
6
12
15
18
20
25
27
30
32
35
36
人数
1
1
7
18
10
5
2
2
1
1
2
相关试题

