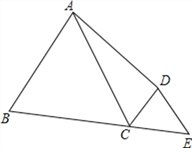
【题目】如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:
(1)由已知条件AB=AD,∠BAD=60°,可知:△ABD是 三角形;
(2)同理由已知条件∠BCD=120°得到∠DCE= ,且CE=CD,可知 ;
(3)要证BC+DC=AC,可将问题转化为两条线段相等,即 = ;请你先完成思路点拨,再进行证明:
参考答案:
【答案】(1)等边.(2)60°,△DCE是等边三角形.(3)BE=AC,证明见解析。
【解析】分析:(1)连接BD,根据等边三角形判定推出即可;(2)求出∠DCE=60°,得到等边三角形DCE即可;(3)根据等边三角形性质推出AD=BD,CD=DE,∠ADB=∠CDE=60°,推出∠ADC=∠BDE,证△ADC≌△BDE即可;
本题解析:(1)等边.(2)60°,△DCE是等边三角形.
(3)BE=AC.
证明:连接BD,
∵AB=AD,∠BAD=60°,∴△ABD是等边三角形,
∵∠BCD=120°,
∴∠DCE=180°-∠BCD=180°-120°=60°,
∵CE=CD,
∴△DCE是等边三角形,
∵等边三角形ABD和DCE,
∴AD=BD,CD=DE,∠ADB=∠CDE=60°,
∴∠ADB+∠BDC=∠CDE+∠BDC,
即∠ADC=∠BDE,
在△ADC和△BDE中,AD=BD,∠ADC=∠BDE, DC=DE,
∴△ADC≌△BDE,
∴AC=BE=BC+CE =BC+DC,
∴BC+DC=AC

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2x2)3的结果是( )
A.﹣2x5
B.﹣8x6
C.﹣2x6
D.﹣8x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,m,n是一元二次方程
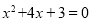 的两个实数根,且|m|<|n|,抛物线
的两个实数根,且|m|<|n|,抛物线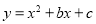 的图象经过点A(m,0),B(0,n),如图所示.
的图象经过点A(m,0),B(0,n),如图所示.(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为
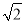 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(1,2)关于原点的对称点P′的坐标为( )
A. (2,1) B. (﹣1,﹣2) C. (1,﹣2) D. (﹣2,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书每本定价8元,若购书不超过10本,按原价付款;若一次购书10本以上,超过10本部分按八折付款.设一次购书数量为x本(x>10),则付款金额为( )
A.6.4x元
B.(6.4x+80)元
C.(6.4x+16)元
D.(144﹣6.4x)元 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的对话。
小红:“售货员,我要买些梨。”
售货员说:“小红,你上次买的那种梨卖完了,我们还没来得及进货,我建议你这次买些新进的苹果,价格比梨贵一点,不过这批苹果的味道挺好哟!”
小红:“好,这次和上次一样,也花30元。”
对照前后两次的电脑小票,小红发现,每千克苹果的单价是梨的1.5倍,买的苹果的重量比梨轻2.5Kg。
试根据上面的对话和小红的发现,分别求出苹果和梨的单价。
相关试题

