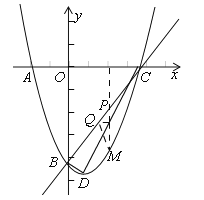
【题目】已知,m,n是一元二次方程![]() 的两个实数根,且|m|<|n|,抛物线
的两个实数根,且|m|<|n|,抛物线![]() 的图象经过点A(m,0),B(0,n),如图所示.
的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.

参考答案:
【答案】(1)![]() ;(2)△BCD是直角三角形;(3)S=
;(2)△BCD是直角三角形;(3)S=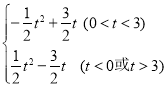 .
.
【解析】
试题分析:(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先解方程求出抛物线与x轴的交点,再判断出△BOC和△BED都是等腰直角三角形,从而得到结论;
(3)先求出QF=1,再分两种情况,当点P在点M上方和下方,分别计算即可.
试题解析:解(1)∵![]() ,∴
,∴![]() ,
,![]() ,∵m,n是一元二次方程
,∵m,n是一元二次方程![]() 的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线
的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线![]() 的图象经过点A(m,0),B(0,n),∴
的图象经过点A(m,0),B(0,n),∴![]() ,∴
,∴![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)令y=0,则![]() ,∴
,∴![]() ,
,![]() ,∴C(3,0),∵
,∴C(3,0),∵![]() =
=![]() ,∴顶点坐标D(1,﹣4),过点D作DE⊥y轴,∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形;
,∴顶点坐标D(1,﹣4),过点D作DE⊥y轴,∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形;
(3)如图,∵B(0,﹣3),C(3,0),∴直线BC解析式为y=x﹣3,∵点P的横坐标为t,PM⊥x轴,∴点M的横坐标为t,∵点P在直线BC上,点M在抛物线上,∴P(t,t﹣3),M(t,![]() ),过点Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=
),过点Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=![]() ,∴QF=1.
,∴QF=1.
①当点P在点M上方时,即0<t<3时,PM=t﹣3﹣(![]() )=
)=![]() ,∴S=
,∴S=![]() PM×QF=
PM×QF=![]() =
=![]() ,②如图3,当点P在点M下方时,即t<0或t>3时,PM=
,②如图3,当点P在点M下方时,即t<0或t>3时,PM=![]() ﹣(t﹣3)=
﹣(t﹣3)=![]() ,∴S=
,∴S=![]() PM×QF=
PM×QF=![]() (
(![]() )=
)=![]() .
.
综上所述,S=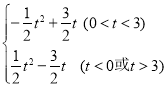 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在
 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+2a=1,则代数式1﹣2(a2+2a)的值为( )
A. 0 B. 1 C. ﹣1 D. ﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2x2)3的结果是( )
A.﹣2x5
B.﹣8x6
C.﹣2x6
D.﹣8x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
-
科目: 来源: 题型:
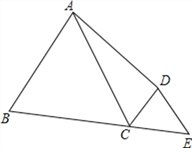
查看答案和解析>>【题目】如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:
(1)由已知条件AB=AD,∠BAD=60°,可知:△ABD是 三角形;
(2)同理由已知条件∠BCD=120°得到∠DCE= ,且CE=CD,可知 ;
(3)要证BC+DC=AC,可将问题转化为两条线段相等,即 = ;请你先完成思路点拨,再进行证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(1,2)关于原点的对称点P′的坐标为( )
A. (2,1) B. (﹣1,﹣2) C. (1,﹣2) D. (﹣2,﹣1)
相关试题

