【题目】如图,线段AB 是⊙O的直径,弦CD⊥AB于点H,点M是弧CBD 上任意一点,AH=2,CH=4.
(1)求⊙O 的半径r 的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O 于点 N,连接BN交CE于点 F,求HE![]() HF的值.
HF的值.


参考答案:
【答案】(1)5;(2)![]() ;(3)16
;(3)16
【解析】(1)在Rt△COH中,利用勾股定理即可解决问题;
(2)只要证明∠CMD=△COA,求出sin∠COA即可;
(3)由△EHM∽△NHF,推出![]() ,推出HEHF=HMHN,又HMHN=AHHB,推出HEHF=AHHB,由此即可解决问题.
,推出HEHF=HMHN,又HMHN=AHHB,推出HEHF=AHHB,由此即可解决问题.
(1)连接OC,
在Rt△COH中,
∵CH=4,OH=r-2,OC=r.
∴ (r-2)2+42=r2.
∴ r=5;
(2)∵弦CD与直径AB垂直,
∴![]() ,
,
∴ ∠AOC=![]() ∠COD,
∠COD,
∴∠CMD=![]() ∠COD,
∠COD,
∴ ∠CMD=∠AOC,
∴sin∠CMD=sin∠AOC,
在Rt△COH中,
∴sin∠AOC=![]() ,
,
∴sin∠CMD=![]() ;
;
(3)连接AM,
∴∠AMB=90°,
在Rt△AMB中,
∴∠MAB+∠ABM=90°,
在Rt△EHB中,
∴∠E+∠ABM=90°,
∴∠MAB=∠E,
∵![]() ,
,
∴∠MNB=∠MAB=∠E,
∵∠EHM=∠NHF,
∴△EHM∽△NHF,
∴![]() ,
,
∴HEHF=HMHN,
∵AB与MN交于点H,
∴HMHN=HAHB=HA(2r-HA)=2×(10-2)=16,
∴HEHF=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )
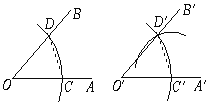
A.SAS B.ASA C.AAS D.SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明每天早上要在7:50之前赶到距家1000 m的学校.小明每天以80 m/min的速度出发.
(1)小明出发5 min后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以 180 m/min的速度去追小明,并且在途中追上了小明.爸爸追上小明用了多长时间?
(2)小明出发 8 min后,妈妈急于上班,门锁碰上时,发现忘带手机和钥匙,于是立即以120 m/min的速度去追小明拿钥匙.请问妈妈能否在小明进学校前追上小明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
已知:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
试说明:∠EGF=90°.
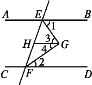
解:因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+ =180°( ).
又因为EG平分∠BEF(已知),
所以∠1=
 ∠ ( ).
∠ ( ).又因为FG平分∠EFD(已知),
所以∠2=
 ∠ ( ),
∠ ( ),所以∠1+∠2=
 ( + ).
( + ).所以∠1+∠2=90°.
所以∠3+∠4=90°( ),即∠EGF=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把等腰直角三角形的三角板按如图所示的方式立在桌面上,顶点A顶着桌面,若另两个顶点分别距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离即DE的长为( )

A. 4cm B. 6cm C. 8cm D. 求不出来
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知2a﹣1的平方根是±3,3a+b﹣9的立方根是2,c是
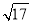 的整数部分,求a+2b+c的值.
的整数部分,求a+2b+c的值.(2)有四个实数分别为32,
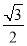 ,
,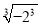 ,
,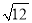 .
.①请你计算其中有理数的和.
②若x﹣2是①中的和的平方,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(3a﹣8,a﹣1),分别根据下列条件求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点N坐标为(1,6),并且直线MN∥y轴.
相关试题

