【题目】如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
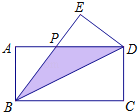
(1)BD= ;
(2)点P到BD的距离是 .
参考答案:
【答案】(1)2![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)由勾股定理直接得出;
(2)设AP=x,证出△ABP≌△EDP,可知EP=x,PD=8﹣x,根据翻折不变性,可知ED=DC=AB=2,然后在Rt△PED中,利用勾股定理求出x,再由三角形的面积即可求出结论.
解:(1)∵四边形ABCD是长方形,
∴∠C=90°,
∴BD=![]() =
=![]() =2
=2![]() ,
,
故答案为2![]() ;
;
(2)在△APB与△DEP中,
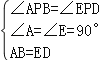 ,
,
∴△APB≌△DEP,
∴AP=EP,
设AP=x,可知EP=x,PD=4﹣x,
∴在Rt△PED中,
x2+22=(4﹣x)2,
解得x=![]() .
.
即AP=![]() ,
,
∴PD=4﹣![]() =
=![]() ,
,
∴△BDP的面积=![]() ×
×![]() ×2=
×2=![]() ×2
×2![]() 点P到BD的距离,
点P到BD的距离,
∴点P到BD的距离=![]() ,
,
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,那么k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在学校体育活动时间不低于1h”,为此,某市就“每天在校体育活动时间”的问题随机调查了辖区内320名初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h;
B组:0.5h≤t<1h;
C组:1h≤t<1.5h;
D组:1.5h≤t
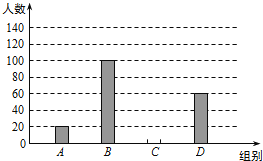
请根据上述信息解答下列问题:
(1)C组的人数是 ;请在图中补全条形图.
(2)本次调查数据的中位数落在 组内;
(3)若该市辖区内约有32000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?(要求写出必要的过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.

(1) 求证:PA是⊙O的切线;
(2) 若
 ,且OC=4,求PA的长.
,且OC=4,求PA的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,根据图中数据完成填空,再按要求答题:
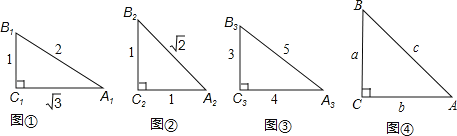
sin2A1+sin2B1= ;sin2A2+sin2B2= ;sin2A3+sin2B3= .
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B= .
(2)如图④,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,利用三角函数的定义和勾股定理,证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣7的相反数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于ABCD的叙述,正确的是( )
A.若AB⊥BC,则ABCD是菱形 B.若AC⊥BD,则ABCD是正方形
C.若AC=BD,则ABCD是矩形 D.若AB=AD,则ABCD是正方形
相关试题

