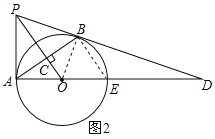
【题目】如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.

(1) 求证:PA是⊙O的切线;
(2) 若![]() ,且OC=4,求PA的长.
,且OC=4,求PA的长.
参考答案:
【答案】(1)证明见解析;(2)3![]() .
.
【解析】
试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;
(2)连接BE,由![]() ,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.
,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.
试题解析:(1)连接OB,则OA=OB,

∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵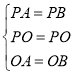 ,
,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,
即PA⊥OA,
∴PA是⊙O的切线;
(2)连接BE,
∵![]() ,且OC=4,
,且OC=4,
∴AC=6,
∴AB=12,
在Rt△ACO中,
由勾股定理得:AO=![]() ,
,
∴AE=2OA=4![]() ,OB=OA=2
,OB=OA=2![]() ,
,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OC![]() PC,
PC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP=![]() =3
=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种服装原售价为100元,由于换季连续两次降价处理,现按64元的售价销售.已知两次降价的百分率相同,设每次降价的百分率为x,则可列方程
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,那么k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在学校体育活动时间不低于1h”,为此,某市就“每天在校体育活动时间”的问题随机调查了辖区内320名初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h;
B组:0.5h≤t<1h;
C组:1h≤t<1.5h;
D组:1.5h≤t
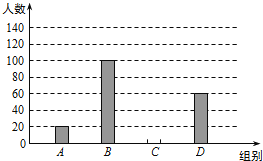
请根据上述信息解答下列问题:
(1)C组的人数是 ;请在图中补全条形图.
(2)本次调查数据的中位数落在 组内;
(3)若该市辖区内约有32000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?(要求写出必要的过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
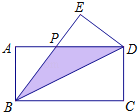
(1)BD= ;
(2)点P到BD的距离是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,根据图中数据完成填空,再按要求答题:
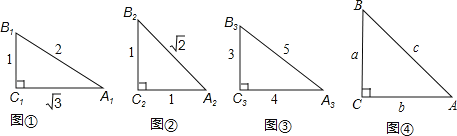
sin2A1+sin2B1= ;sin2A2+sin2B2= ;sin2A3+sin2B3= .
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B= .
(2)如图④,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,利用三角函数的定义和勾股定理,证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣7的相反数是_____.
相关试题

