【题目】已知直线a:y=2x+4分别与x、y轴交于点A、C.将直线a竖直向下平移7个单位后得到直线b,直线b交直线AD:y=x+2于点E.
(1)若点Q为直线x轴上一动点,是否存在点Q,使△QDE的周长最小,若存在,求△QDE周长的最小值及点Q的坐标:
(2)已知点M是第一象限直线a上的任意一点,过点M作直线c⊥x轴,交直线b于点N,H为直线AD上任意一点,是否存在点M,使得△MNH成为等腰直角三角形?若存在,请直接写出点H的坐标.

参考答案:
【答案】(1)存在,Q(![]() ,0),∴△DEQ的周长的最小值为5
,0),∴△DEQ的周长的最小值为5![]() ;(2)存在,满足条件的点H的坐标为(12,14)或(
;(2)存在,满足条件的点H的坐标为(12,14)或(![]() ,
,![]() ).
).
【解析】
(1)如图1中,存在.首先确定点D,点E的坐标,作点D关于x轴的对称点D′,连接ED′交x轴于Q,连接DQ,此时△DEQ的周长最小.
(2)如图2中,存在.当点N与E(5,7)重合时,作MH∥x轴交直线y=x+2于H,此时△MNH是等腰直角三角形,取EH的中点H′,连接MH′,此时△MNH′也是等腰直角三角形.
解:(1)存在.
理由:∵直线y=2x+4分别与x、y轴交于点A、C,
令x=0,得到y=4,令y=0,得到x=﹣2,
∴A(﹣2,0),C(0,4),
∵直线y=2x+4竖直向下平移7个单位后得到直线b,
∴直线b的解析式为y=2x﹣3,
∵直线y=x+2交x轴于A,交y轴于D,
令x=0,得到y=2,
∴D(0,2),
由![]() ,解得
,解得![]() ,
,
∴E(5,7),
如图1中,作点D关于x轴的对称点D′,连接ED′交x轴于Q,连接DQ,此时△DEQ的周长最小.

∵D′(0,﹣2),E(5,7),
∴直线DE的解析式为y=![]() x﹣2,
x﹣2,
∴Q(![]() ,0),
,0),
![]() ,
,![]() ,
,
∴△DEQ的周长的最小值=DE+DQ+EQ=DE+QD′+QE=DE+ED′=5![]() ;
;
(2)如图2中,存在.

理由:当点N与E(5,7)重合时,作MH∥x轴交直线y=x+2于H,此时△MNH是等腰直角三角形,取EH的中点H′,连接MH′,此时△MNH′也是等腰直角三角形,
∵M(5,14),MH∥x轴,
∴H(12,14),
∵E(5,7),EH′=HH′,
∴H′(![]() ,
,![]() ).
).
综上所述,满足条件的点H的坐标为(12,14)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列条件中,能判断直线L1∥L2的是( )

A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180
 D. ∠2=∠4
D. ∠2=∠4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图抛物线与x轴分别交于A、B两点,顶点C在y轴负半轴上,也在正方形ADEB的边上,已知正方形ADEB的边长为2,若正方形FGMN的顶点F、G落在x轴上,顶点M、N落在图中的抛物线上,则正方形FGMN的边长为.

-
科目: 来源: 题型:
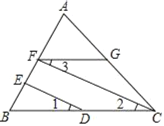
查看答案和解析>>【题目】请你完成下面的证明:
已知:如图,∠GFB+∠B=180°,∠1=∠3,
求证:FC∥ED.
证明:∵∠GFB+∠B=180°
∴FG∥BC( )
∴∠3= ( ),
又∵∠1=∠3(已知)
∴∠1= (等量代换)
∴FC∥ED( )
-
科目: 来源: 题型:
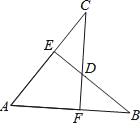
查看答案和解析>>【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c,当x取1时,函数有最大值为3,且函数的图象经过点(-2,0)。
(1)求这个二次函数的解析式;
(2)根据图象直接写出函数值y大于零时x的取值范围
相关试题

