【题目】已知一次函数y1=x+m的图象与反比例函数![]() 的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.

(1)求一次函数的解析式;
(2)已知双曲线在第一象限上有一点C到y轴的距离为3,求△ABC的面积.
参考答案:
【答案】(1)y1=x+5 (2)21
【解析】
试题分析:(1)首先根据x>1时,y1>y2,0<x<1时,y1<y2确定点A的横坐标,然后代入反比例函数解析式求出点A的纵坐标,从而得到点A的坐标,再利用待定系数法求直线解析式解答;
(2)根据点C到y轴的距离判断出点C的横坐标,代入反比例函数解析式求出纵坐标,从而得到点C的坐标,过点C作CD∥x轴交直线AB于D,求出点D的坐标,然后得到CD的长度,再联立一次函数与双曲线解析式求出点B的坐标,然后△ABC的面积=△ACD的面积+△BCD的面积,列式进行计算即可得解.
解:(1)∵当x>1时,y1>y2;当0<x<1时,y1<y2,
∴点A的横坐标为1,
代入反比例函数解析式,![]() =y,
=y,
解得y=6,
∴点A的坐标为(1,6),
又∵点A在一次函数图象上,
∴1+m=6,
解得m=5,
∴一次函数的解析式为y1=x+5;
(2)∵第一象限内点C到y轴的距离为3,
∴点C的横坐标为3,
∴y=![]() =2,
=2,
∴点C的坐标为(3,2),
过点C作CD∥x轴交直线AB于D,
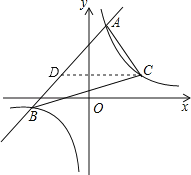
则点D的纵坐标为2,
∴x+5=2,
解得x=﹣3,
∴点D的坐标为(﹣3,2),
∴CD=3﹣(﹣3)=3+3=6,
点A到CD的距离为6﹣2=4,
联立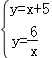 ,
,
解得![]() (舍去),
(舍去),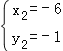 ,
,
∴点B的坐标为(﹣6,﹣1),
∴点B到CD的距离为2﹣(﹣1)=2+1=3,
S△ABC=S△ACD+S△BCD=![]() ×6×4+
×6×4+![]() ×6×3=12+9=21.
×6×3=12+9=21.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则
 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 ,同理有:
,同理有:  ,所以
,所以 .
.即:在一个锐角三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)某次巡逻中,如图(3),我渔政船在C处测得钓鱼岛A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政船距钓鱼岛A的距离AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初一年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都7.5折收费.
(1)若有m名学生,用代数式表示两种优惠方案各需多少元?
(2)当m=70时,采用哪种方案优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级所有学生参加2015年初中毕业生升学体育测试,为了解情况,从中抽取了部分学生的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

(1)计算一共抽取了多少名学生的测试成绩并将条形统计图补充完整;
(2)在扇形统计图中,等级C对应的圆心角的度数为多少度?
(3)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学活动小组在做角的拓展图形练习时,经历了如下过程:

(1)操作发现:点
 为直线
为直线 上一点,过点
上一点,过点 作射线
作射线 ,使
,使 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点 处,一边
处,一边 在射线
在射线 上,另一边
上,另一边 在直线
在直线 的下方,如图:将图1中的三角板绕点
的下方,如图:将图1中的三角板绕点 旋转,当直角三角板的
旋转,当直角三角板的 边在
边在 的内部,且恰好平分
的内部,且恰好平分 时,如图2.则下列结论正确的是 (填序号即可).
时,如图2.则下列结论正确的是 (填序号即可).①
 ②
② ③
③ 平分
平分 ④
④ 的平分线在直线
的平分线在直线 上
上(2)数学思考:同学们在操作中发现,当三角板绕点
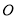 旋转时,如果直角三角板的
旋转时,如果直角三角板的 边在
边在 的内部且另一边
的内部且另一边 在直线AB的下方,那么
在直线AB的下方,那么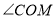 与
与 的差不变,请你说明理由;如果直角三角板的
的差不变,请你说明理由;如果直角三角板的 、
、 边都在
边都在 的内部,那么
的内部,那么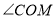 与
与 的和不变,请直接写出
的和不变,请直接写出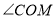 与
与 的和,不要求说明理由.
的和,不要求说明理由.(3)类比探索:三角板绕点
 继续旋转,当直角三角板的
继续旋转,当直角三角板的 边在
边在 的内部时,如图3,求
的内部时,如图3,求 与
与 相差多少度?为什么?
相差多少度?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.

(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过
 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=
 ,AH=3
,AH=3 ,求EM的值.
,求EM的值.
相关试题

