【题目】如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE= ![]() .直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是 .
.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是 . 
参考答案:
【答案】![]() 或
或 ![]()
【解析】解:由tan∠AOE= ![]() ,可设A、B点坐标分别为(2m,3m)、(2n,3n),
,可设A、B点坐标分别为(2m,3m)、(2n,3n),
∵AD∥OC,
∴∠ADB=∠OCB,∠DAB=∠COA,
∴△BAD∽△BOC.
①当点A在第一象限时,如图1所示.
∵OC=2AD,
∴D点为线段BC的平分线,
∵C(0,c),B(2n,3n),
∴D点横坐标为 ![]() =n,
=n,
由题意知A、D点均在抛物线的对称轴上,
∴n=2m,
∴B点坐标为(4m,6m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有  ,
,
解得 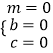 ,或
,或  ,
,
∵c>0,
∴c= ![]() ;
;
②当点A在第四象限时,如图2所示.
∵OC=2AD,
∴B点为线段CD的三等分点,
∵C(0,c),B(2n,3n),
∴D点横坐标为2n× ![]() =3n,
=3n,
由题意知A、D点均在抛物线的对称轴上,
∴3n=2m,
∴B点坐标为( ![]() m,2m),
m,2m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有 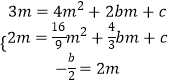 ,
,
解得 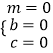 ,或
,或 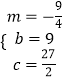 ,
,
∵c>0,
∴c= ![]() .
.
所以答案是: ![]() 或
或 ![]() .
.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
 ;
; ;
; ;
; 如果方程
如果方程 与方程
与方程 的解相同,求
的解相同,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把
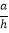 的值叫做这个菱形的“形变度”;例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:
的值叫做这个菱形的“形变度”;例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2: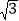 ;如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A'E'F',若这个菱形的“形变度”k=
;如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A'E'F',若这个菱形的“形变度”k= ,则
,则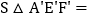 _______;
_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如图两幅统计图(不完整).
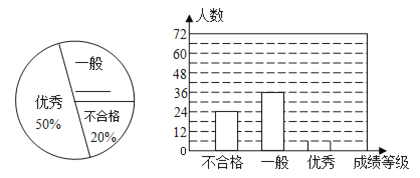
请你根据图中所给的信息解答下列问题:
(1)这次测试,一共抽取了名学生;
(2)请将以上两幅统计图补充完整;(注:扇形图补百分比,条形图补“优秀”人数与高度);
(3)若“一般”和“优秀”均被视为达标成绩,该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王强参加了一场3000米的赛跑,他以6米/秒的速度跑了一段路程,又以4 米/秒的速度跑完了其余的路程,一共花了10分钟,王强以6米/ 秒的速度跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.
(1)求∠CAE的度数;
(2)取AB边的中点F,连接CF、CE,试说明四边形AFCE是矩形.

相关试题

